XGBoost
算法思想
在决策树中,我们知道一个样本往左边分或者往右边分,最终到达叶子结点,这样来进行一个分类任务。 其实也可以做回归任务。
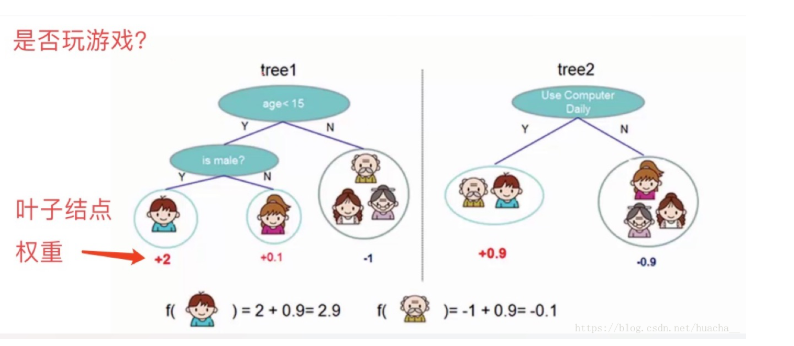
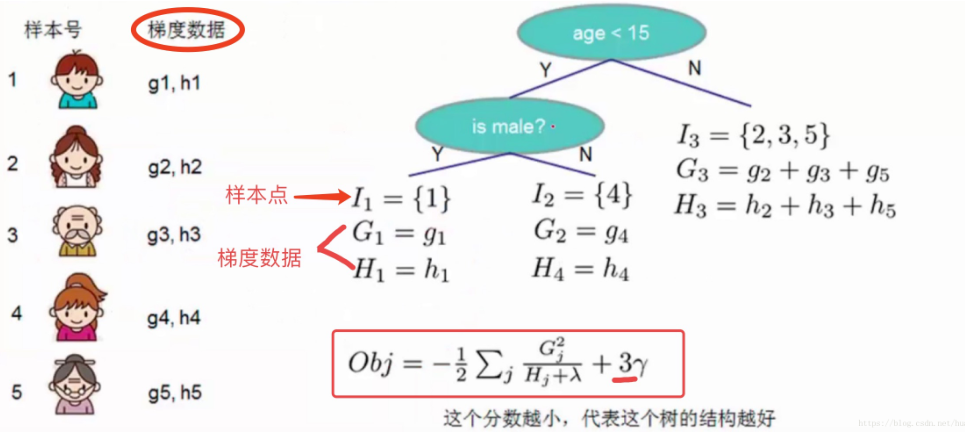
看上面一个图例左边:有5个样本,现在想看下这5个人愿不愿意去玩游戏,这5个人现在都分到了叶子结点里面,对不同的叶子结点分配不同的权重项,正数代表这个人愿意去玩游戏,负数代表这个人不愿意去玩游戏。所以我们可以通过叶子结点和权值的结合,来综合的评判当前这个人到底是愿意还是不愿意去玩游戏。上面「tree1」那个小男孩它所处的叶子结点的权值是+2(可以理解为得分)。
用单个决策树好像效果一般来说不是太好,或者说可能会太绝对。通常我们会用一种集成的方法,就是一棵树效果可能不太好,用两棵树呢?
看图例右边的「tree2」,它和左边的不同在于它使用了另外的指标,出了年龄和性别,还可以考虑使用电脑频率这个划分属性。通过这两棵树共同帮我们决策当前这个人愿不愿意玩游戏,小男孩在「tree1」的权值是+2,在「tree2」的权值是+0.9, 所以小男孩最终的权值是+2.9(可以理解为得分是+2.9)。老爷爷最终的权值也是通过一样的过程得到的。
所以说,我们通常在做分类或者回归任务的时候,需要想一想一旦选择用一个分类器可能表达效果并不是很好,那么就要考虑用这样一个集成的思想。上面的图例只是举了两个分类器,其实还可以有更多更复杂的弱分类器,一起组合成一个强分类器。
XGBoost原理
XGBoost的集成表示是什么?怎么预测?求最优解的目标是什么?看下图的说明你就能一目了然。

在XGBoost里,每棵树是一个一个往里面加的,每加一个都是希望效果能够提升,下图就是XGBoost这个集成的表示(核心)。

一开始树是0,然后往里面加树,相当于多了一个函数,再加第二棵树,相当于又多了一个函数…等等,这里需要保证加入新的函数能够提升整体对表达效果。提升表达效果的意思就是说加上新的树之后,目标函数(就是损失)的值会下降。
如果叶子结点的个数太多,那么过拟合的风险会越大,所以这里要限制叶子结点的个数,所以在原来目标函数里要加上一个惩罚项「omega(ft)」。

这里举个简单的例子看看惩罚项「omega(ft)」是如何计算的:
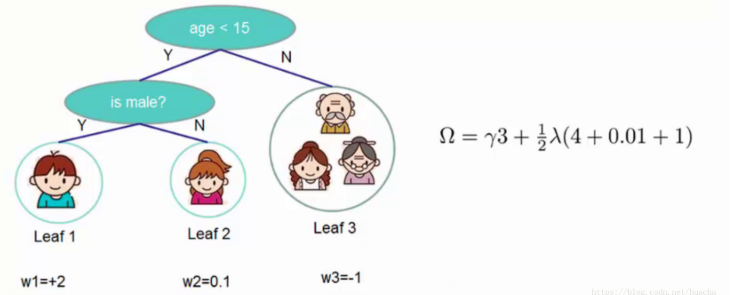
一共3个叶子结点,权重分别是2,0.1,-1,带入「omega(ft)」中就得到上面图例的式子,惩罚力度和「lambda」的值人为给定。
XGBoost算法完整的目标函数见下面这个公式,它由自身的损失函数和正则化惩罚项「omega(ft)」相加而成。
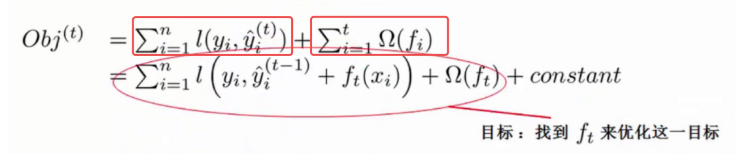
上图中的constant就是前t-1棵树的复杂度,再忍耐一会儿,我们就会知道如何衡量树的复杂度了,暂时忽略它。
假如我们使用的损失函数是MSE,那么上述表达式会变成这个样子:
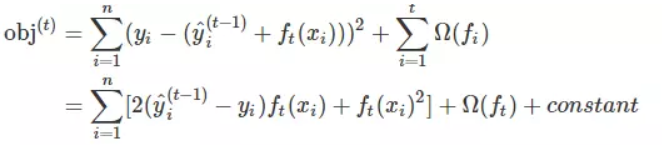
这个式子非常漂亮,因为它含有f_t(x_i)的一次式和二次式,而且一次式项的系数是残差。你可能好奇,为什么有一次式和二次式就漂亮,因为它会对我们后续的优化提供很多方便,继续前进你就明白了。
注意:是什么?它其实就是的某个叶子节点的值。之前我们提到过,叶子节点的值是可以作为模型的参数的
但是对于其他的损失函数,我们未必能得出如此漂亮的式子,所以,对于一般的损失函数,我们需要将其作泰勒二阶展开,如下所示:
![n obj(t) — 1 —hift2@i)] -4- Q(ft) -4- constant 2 ](file:///C:/Users/gaoming/AppData/Local/Temp/msohtmlclip1/01/clip_image009.png)
其中:
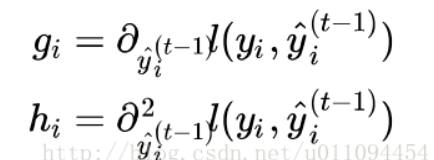
这里有必要再明确一下,和的含义。怎么理解呢?现有t-1棵树是不是?这t-1棵树组成的模型对第i个训练样本有一个预测值是不是?这个与第i个样本的真实标签肯定有差距是不是?这个差距可以用,)这个损失函数来衡量是不是?现在和的含义你已经清楚了是不是?
如果你还是觉得抽象,我们来看一个具体的例子,假设我们正在优化第11棵CART树,也就是说前10棵 CART树已经确定了。这10棵树对样本(=1)的预测值是=-1,假设我们现在是做分类,我们的损失函数是
![L(O) E [Yi In(l + e¯ji) + (I — yt•) In(l + eût)]](/2019/09/11/XGBoost/clip_image013.png)
在=1时,损失函数变成了
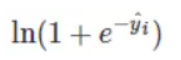
我们可以求出这个损失函数对于的梯度,如下所示:
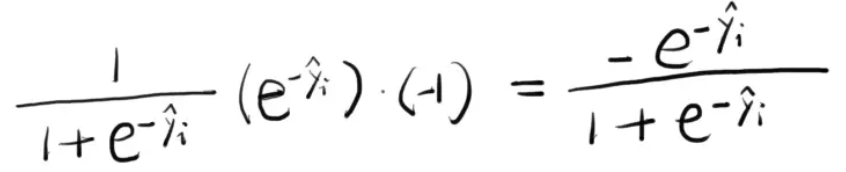
将 =-1代入上面的式子,计算得到-0.27。这个-0.27就是。该值是负的,也就是说,如果我们想要减小这10棵树在该样本点上的预测损失,我们应该沿着梯度的反方向去走,也就是要增大的值,使其趋向于正,因为我们的=1就是正的
来,答一个小问题,在优化第t棵树时,有多少个和要计算?嗯,没错就是各有N个,N是训练样本的数量。如果有10万样本,在优化第t棵树时,就需要计算出个10万个和。感觉好像很麻烦是不是?但是你再想一想,这10万个之间是不是没有啥关系?是不是可以并行计算呢?聪明的你想必再一次感受到了,为什么xgboost会辣么快!
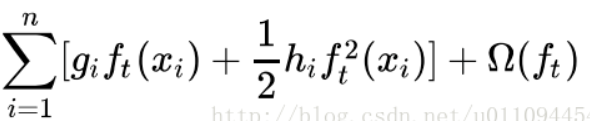
好,现在我们来审视下这个式子,哪些是常量,哪些是变量。式子最后有一个constant项,聪明如你,肯定猜到了,它就是前t-1棵树的正则化项。(,)也是常数项。剩下的三个变量项分别是第t棵CART树的一次式,二次式,和整棵树的正则化项。再次提醒,这里所谓的树的一次式,二次式,其实都是某个叶子节点的值的一次式,二次式
我们的目标是让这个目标函数最小化,常数项显然没有什么用,我们把它们去掉,就变成了下面这样:
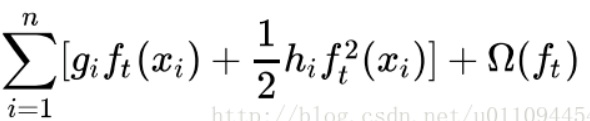
好,现在我们可以回答之前的一个问题了,为什么一次式和二次式显得那么漂亮。因为这些一次式和二次式的系数是和,而和可以并行地求出来。而且,和是不依赖于损失函数的形式的,只要这个损失函数二次可微就可以了。这有什么好处呢?好处就是xgboost可以支持自定义损失函数,只需满足二次可微即可。
模型正则化项
上面的式子已然很漂亮,但是,后面的Ω(ft)仍然是云遮雾罩,不清不楚。现在我们就来定义如何衡量一棵树的正则化项。这个事儿并没有一个客观的标准,可以见仁见智。为此,我们先对CART树作另一番定义,如下所示:
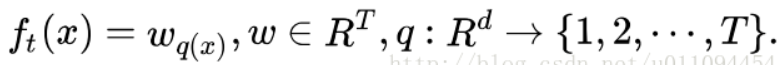
需要解释下这个定义,首先,一棵树有T个叶子节点,这T个叶子节点的值组成了一个T维向量w,q(x)是一个映射,用来将样本映射成1到T的某个值,也就是把它分到某个叶子节点,q(x)其实就代表了CART树的结构。w_q(x)自然就是这棵树对样本x的预测值了。
有了这个定义,xgboost就使用了如下的正则化项:
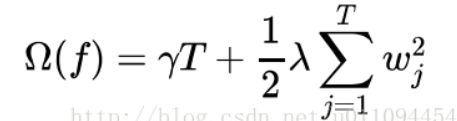
注意:这里出现了γ和λ,这是xgboost自己定义的,在使用xgboost时,你可以设定它们的值,显然,γ越大,表示越希望获得结构简单的树,因为此时对较多叶子节点的树的惩罚越大。λ越大也是越希望获得结构简单的树。
为什么xgboost要选择这样的正则化项?很简单,好使!效果好才是真的好。
见证奇迹的时刻
至此,我们关于第t棵树的优化目标已然很清晰,下面我们对它做如下变形,请睁大双眼,集中精力:
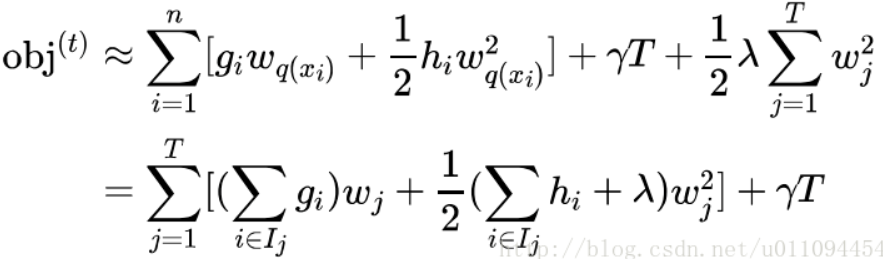
这里需要停一停,认真体会下。代表什么?它代表一个集合,集合中每个值代表一个训练样本的序号,整个集合就是被第t棵CART树分到了第j个叶子节点上的训练样本。理解了这一点,再看这步转换,其实就是内外求和顺序的改变。
进一步,我们可以做如下简化:
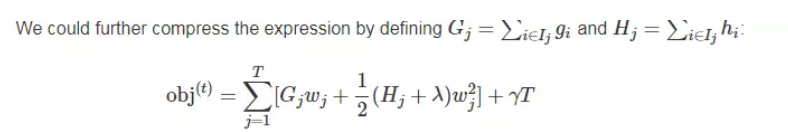
其中的和应当是不言自明了。
对于第t棵CART树的某一个确定的结构(可用q(x)表示),所有的和都是确定的。而且上式中各个叶子节点的值之间是互相独立的。上式其实就是一个简单的二次式,我们很容易求出各个叶子节点的最佳值以及此时目标函数的值
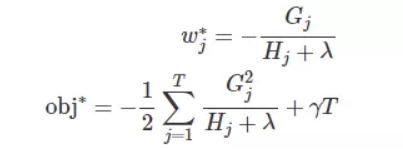
obj代表了什么呢?
它表示了这棵树的结构有多好,值越小,代表这样结构越好!也就是说,它是衡量第t棵CART树的结构好坏的标准。注意注意注意~,这个值仅仅是用来衡量结构的好坏的,与叶子节点的值可是无关的。为什么?请再仔细看一下obj的推导过程。obj只和和和T有关,而它们又只和树的结构(q(x))有关,与叶子节点的值可是半毛关系没有。如下图所示
Note:这里,我们对给出一个直觉的解释,以便能获得感性的认识。我们假设分到j这个叶子节点上的样本只有一个。那么,就变成如下这个样子:
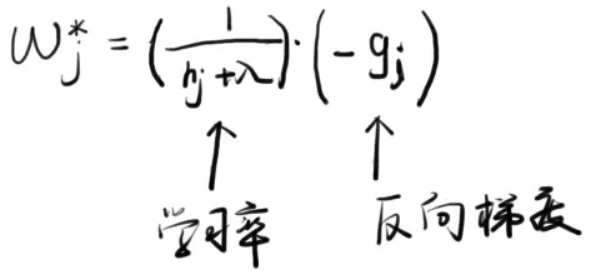
这个式子告诉我们,的最佳值就是负的梯度乘以一个权重系数,该系数类似于随机梯度下降中的学习率。观察这个权重系数,我们发现,越大,这个系数越小,也就是学习率越小。越大代表什么意思呢?代表在该点附近梯度变化非常剧烈,可能只要一点点的改变,梯度就从10000变到了1,所以,此时,我们在使用反向梯度更新时步子就要小而又小,也就是权重系数要更小。
7、找出最优的树结构
好了,有了评判树的结构好坏的标准,我们就可以先求最佳的树结构,这个定出来后,最佳的叶子结点的值实际上在上面已经求出来了。
问题是:树的结构近乎无限多,一个一个去测算它们的好坏程度,然后再取最好的显然是不现实的。所以,我们仍然需要采取一点策略,这就是逐步学习出最佳的树结构。这与我们将K棵树的模型分解成一棵一棵树来学习是一个道理,只不过从一棵一棵树变成了一层一层节点而已。如果此时你还是有点蒙,没关系,下面我们就来看一下具体的学习过程。
我们以上文提到过的判断一个人是否喜欢计算机游戏为例子。最简单的树结构就是一个节点的树。我们可以算出这棵单节点的树的好坏程度obj。假设我们现在想按照年龄将这棵单节点树进行分叉,我们需要知道:
1、按照年龄分是否有效,也就是是否减少了obj的值
2、如果可分,那么以哪个年龄值来分。
为了回答上面两个问题,我们可以将这一家五口人按照年龄做个排序。如下图所示:
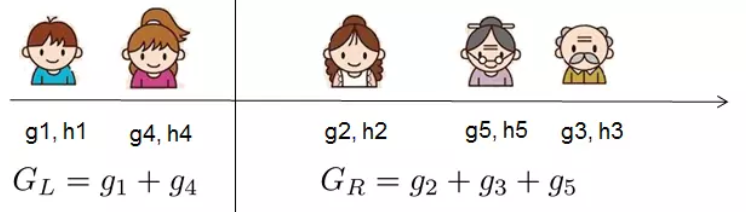
按照这个图从左至右扫描,我们就可以找出所有的切分点,即遍历所有分割,选择变化最大的作为最合适的分割。对每一个确定的切分点,我们衡量切分好坏的标准如下:
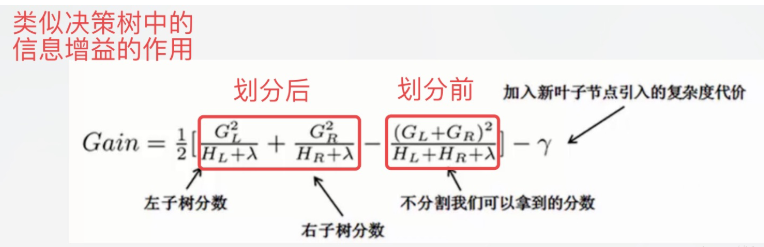
这个Gain实际上就是单节点的obj减去切分后的两个节点的树obj,Gain如果是正的,并且值越大,表示切分后obj越小于单节点的obj,就越值得切分。同时,我们还可以观察到,Gain的左半部分如果小于右侧的γ,则Gain就是负的,表明切分后obj反而变大了。γ在这里实际上是一个临界值,它的值越大,表示我们对切分后obj下降幅度要求越严。这个值也是可以在xgboost中设定的。
扫描结束后,我们就可以确定是否切分,如果切分,对切分出来的两个节点,递归地调用这个切分过程,我们就能获得一个相对较好的树结构。
注意:xgboost的切分操作和普通的决策树切分过程是不一样的。普通的决策树在切分的时候并不考虑树的复杂度,而依赖后续的剪枝操作来控制。xgboost在切分的时候就已经考虑了树的复杂度,就是那个γ参数。所以,它不需要进行单独的剪枝操作。
参考文献
XGBoost——机器学习(理论+图解+安装方法+python代码)