机器学习 神经网络

机器学习基础

机器学习基础

Posted by 高明 on 2019-10-01

机器学习基础

代价函数

损失函数，代价函数，目标函数定义

  • 损失函数Loss Function是定义在单个样本上的，算的是一个样本的误差。
  • 代价函数Cost Function是定义在整个训练集上的，是所有样本误差的平均，也就是损失函数的平均。
  • 目标函数Object Function定义为：最终需要优化的函数。等于经验风险+结构风险（也就是Cost Function + 正则化项）。

为什么代价函数要非负

目标函数存在一个下界，在优化过程当中，如果优化算法能够使目标函数不断减小，根据 单调有界准则，这个优化算法就能证明是收敛有效的。 只要设计的目标函数有下界，基本上都可以，代价函数非负更为方便。

常见代价函数

二次代价函数

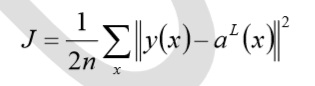
J = lly(x)— aL (xil

其中，J 表示代价函数，x表示样本，y表示实际值，a表示输出值，n表示样本的总数。 使用一个样本为例简单说明，此时二次代价函数为：

(y-a)2 2

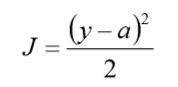
假如使用梯度下降法(Gradient descent)来调整权值参数的大小，权值w和偏置b的梯度推 导如下

img

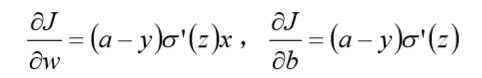
其中，z表示神经元的输入，sigma表示激活函数。权值w和偏置b的梯度跟激活函数的梯度 成正比，激活函数的梯度越大，权值w和偏置b的大小调整得越快，训练收敛得就越快。

神经网络常用的激活函数为sigmoid函数，该函数的曲线如下所示：

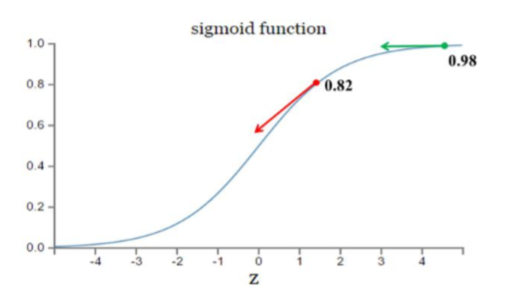
08 06 04 00 .4 .3 sigmoid function 0.82 .2

假设目标是收敛到1.0。0.82离目标比较远，梯度比较大，权值调整比较大。0.98 离目标比较近，梯度比较小，权值调整比较小。调整方案合理。 假如目标是收敛到0。0.82目标比较近，梯度比较大，权值调整比较大。0.98离目标比较远，梯度比较小，权值调整比较小。调整方案不合理。 原因：初始的代价（误差）越大，导致训练越慢。

交叉熵代价函数

— E [y In a + (I — — a)]

其中，J表示代价函数，x表示样本，y表示实际值，a表示输出值，n表示样本的总数。 权值w和偏置b的梯度推导如下：

1 -y) êb

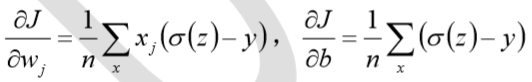
当误差越大时，梯度就越大，权值w和偏置b调整就越快，训练的速度也就越快。 二次代价函数适合输出神经元是线性的情况，交叉熵代价函数适合输出神经元是 S 型函数的情况。

对数似然代价函数

对数释然函数常用来作为softmax 回归的代价函数。深度学习中普遍的做法是将softmax作为最后一层，此时常用的代价函数是对数释然代价函数。 对数似然代价函数与softmax的组合和交叉熵与sigmoid函数的组合非常相似。对数释然代价函数在二分类时可以化简为交叉熵代价函数的形式。

在tensorflow中：

与sigmoid搭配使用的交叉熵函数：tf.nn.sigmoid_cross_entropy_with_logits()。

与softmax搭配使用的交叉熵函数：tf.nn.softmax_cross_entropy_with_logits()。

为什么用交叉熵代替二次代价函数

为什么不用二次方代价函数

权值w和偏置b的偏导数为

img

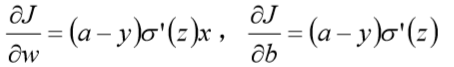
偏导数受激活函数的导数影响，sigmoid 函数导数在输出接近 0 和 1 时非常小，会导致一些实例在刚开始训练时学习得非常慢。

为什么要用交叉熵

交叉熵函数权值w和偏置b的梯度推导为：

1 -y) êb

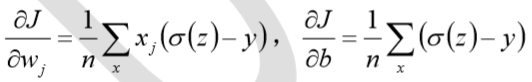
由以上公式可知，权重学习的速度受到sigma(z) - y 的影响，更大的误差，就有更快的学习速度，避免了二次代价函数方程中因sigma'(z)导致的学习缓慢的情况。

损失函数

什么是损失函数？

损失函数（Lossfunction）又叫做误差函数，用来衡量算法的运行情况，估量模型的预测值与真实值Y的不一致程度，是一个非负实值函数,通常使用来表示，损失函数越小，模型的鲁棒性就越好。 损失函数是经验风险函数的核心部分，也是结构风险函数重要组成部分。

常见的损失函数

机器学习通过对算法中的目标函数进行不断求解优化，得到最终想要的结果。分类和回归问题中，通常使用损失函数或代价函数作为目标函数。 损失函数用来评价预测值和真实值不一样的程度。通常损失函数越好，模型的性能也越好。 损失函数可分为经验风险损失函数和结构风险损失函数。经验风险损失函数指预测结果和实际结果的差别，结构风险损失函数是在经验风险损失函数上加上正则项。 下面介绍常用的损失函数：

0-1 损失函数

如果预测值和目标值相等，值为 0，如果不相等，值为 1.

img

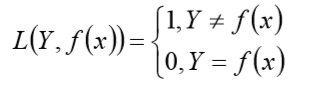
一般的在实际使用中，相等的条件过于严格，可适当放宽条件：

img

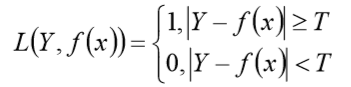
绝对值损失函数

和 0-1 损失函数相似，绝对值损失函数表示为

img

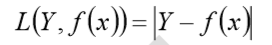
平方损失函数

img

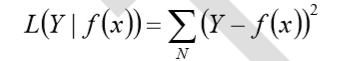
这点可从最小二乘法和欧几里得距离角度理解。最小二乘法的原理是，最优拟合曲线应该 使所有点到回归直线的距离和最小

log 对数损失函数

img

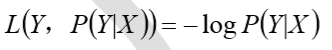
常见的逻辑回归使用的就是对数损失函数，有很多人认为逻辑回归的损失函数是平方损失， 其实不然。逻辑回归它假设样本服从伯努利分布，进而求得满足该分布的似然函数，接着取对数求极值等。逻辑回归推导出的经验风险函数是最小化负的似然函数，从损失函数的角度看， 就是 log 损失函数。

指数损失函数

指数损失函数的标准形式为：

I f exp[— yf(x)]

例如 AdaBoost 就是以指数损失函数为损失函数。

Hinge 损失函数

Hinge 损失函数的标准形式如下：

img

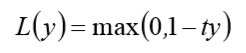
其中 y 是预测值，范围为(-1,1),t 为目标值，其为-1 或 1.

在线性支持向量机中，最优化问题可等价于

img

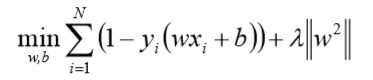
上式相似于下式

img

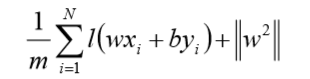
其中$l(wx_i+by_i)$ 是Hinge 损失函数，$||w||^2$可看做为正则化项

逻辑回归为什么使用对数损失函数？

假设逻辑回归模型

_8Tx

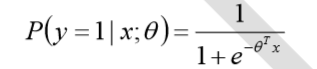
假设逻辑回归模型的概率分布是伯努利分布，其概率质量函数为

img

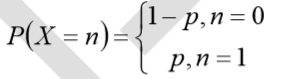
其似然函数为

img

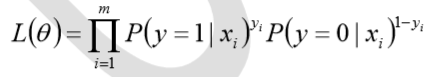
对数似然函数为

img

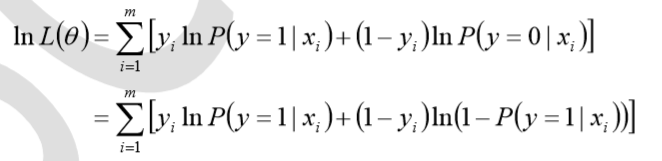
对数函数在单个数据点上的定义为

img

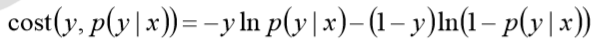
则全局样本损失函数为

img

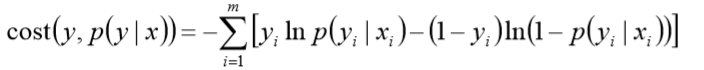
由此可看出，对数损失函数与极大似然估计的对数似然函数本质上是相同的。所以逻辑回 归直接采用对数损失函数。

梯度下降法

直观理解

img

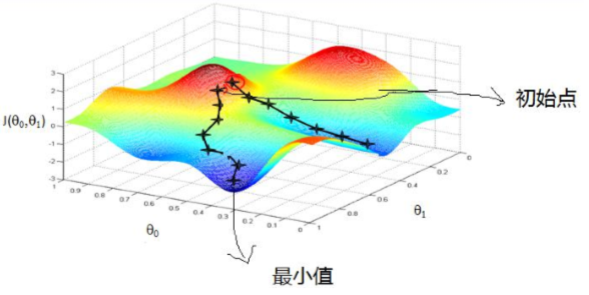
由上图，假如最开始，我们在一座大山上的某处位置，因为到处都是陌生的，不知道下山的路，所以 只能摸索着根据直觉，走一步算一步，在此过程中，每走到一个位置的时候，都会求解当前位置的梯度， 沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位 置沿着最陡峭最易下山的位置走一步。不断循环求梯度，就这样一步步的走下去，一直走到我们觉得已经 到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处。 由此，从上面的解释可以看出，梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。 当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

核心思想归纳

  1. 初始化参数，随机选取取值范围内的任意数；
  2. 迭代操作：
    1. 计算当前梯度；
    2. 修改新的变量；
    3. 计算朝最陡的下坡方向走一步；
    4. 判断是否需要终止，如否，返回 a)；
  3. 得到全局最优解或者接近全局最优解

随机梯度和批量梯度区别

随机梯度下降和批量梯度下降是两种主要梯度下降法，其目的是增加某些限制来加速运算求解。

引入随机梯度下降法与mini-batch梯度下降法是为了应对大数据量的计算而实现一种快速的求解。

下面通过介绍两种梯度下降法的求解思路，对其进行比较。

假设函数为

img

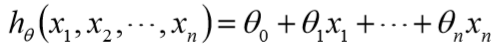
损失函数为

3 3 0 冖

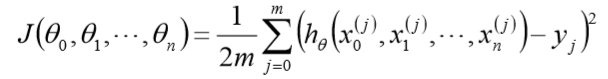
其中，m为样本个数， j为参数个数。

批量梯度下降的求解思路

  • 得到每个$theta$对应的梯度：

1, δθι

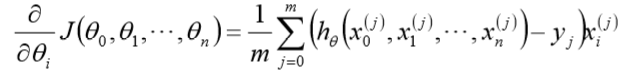
  • 由于是求最小化风险函数，所以按每个参数$theta$的梯度负方向更新$theta_i$ ：

3 3

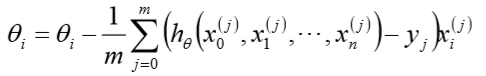
优点
  1. 一次迭代是对所有样本进行计算，此时利用矩阵进行操作，实现了并行。
  2. 由全数据集确定的方向能够更好地代表样本总体，从而更准确地朝向极值所在的方向。当目标函数为凸函数时，BGD一定能够得到全局最优。
缺点
  1. 当样本数目 mm 很大时，每迭代一步都需要对所有样本计算，训练过程会很慢。
  2. 从迭代的次数上来看，BGD迭代的次数相对较少。

随机梯度下降的求解思路

  • 相比批量梯度下降对应所有的训练样本，随机梯度下降法中损失函数对应的是训练集中每个样本的粒度。 损失函数可以写成如下这种形式

2 1

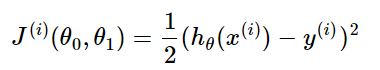
  • 对目标函数求偏导得到每个$theta$对应的梯度：

img

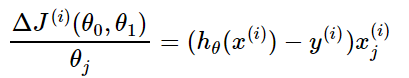
  • 对每个参数 $theta$按梯度方向更新$theta_i$ ：

img

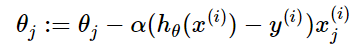
注意：不再有求和符号

优点
  1. 由于不是在全部训练数据上的损失函数，而是在每轮迭代中，随机优化某一条训练数据上的损失函数，这样每一轮参数的更新速度大大加快。
缺点
  1. 准确度下降。由于即使在目标函数为强凸函数的情况下，SGD仍旧无法做到线性收敛。
  2. 可能会收敛到局部最优，由于单个样本并不能代表全体样本的趋势。
  3. 不易于并行实现。

小结

随机梯度下降法、批量梯度下降法相对来说都比较极端，简单对比如下：

批量梯度下降
  1. 采用所有数据来梯度下降
  2. 批量梯度下降法在样本量很大的时候，训练速度慢。
随机梯度下降
  1. 随机梯度下降用一个样本来梯度下降。
  2. 训练速度很快。
  3. 随机梯度下降法仅仅用一个样本决定梯度方向，导致解有可能不是最优。

下面介绍能结合两种方法优点的小批量梯度下降法。

小批量mini-batch梯度下降的求解思路

对于总数为m个样本的数据，根据样本的数据，选取其中的n(1<n<m)个子样本来迭代。 其参数$theta$按梯度方向更新 $theta_i$公式如下:

img

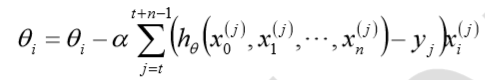
优点
  1. 通过矩阵运算，每次在一个batch上优化神经网络参数并不会比单个数据慢太多
  2. 每次使用一个batch可以大大减小收敛所需要的迭代次数，同时可以使收敛到的结果更加接近梯度下降的效果。(比如上例中的30W，设置batch_size=100时，需要迭代3000次，远小于SGD的30W次)
  3. 可实现并行化
缺点
  1. batch_size的不当选择可能会带来一些问题。

batch_size的选择带来的影响

  1. 在合理地范围内，增大batch_size的好处：
    1. 内存利用率提高了，大矩阵乘法的并行化效率提高
    2. 跑完一次 epoch（全数据集）所需的迭代次数减少，对于相同数据量的处理速度进一步加快
    3. 在一定范围内，一般来说 Batch_Size 越大，其确定的下降方向越准，引起训练震荡越小
  2. 盲目增大batch_size的坏处
    1. 内存利用率提高了，但是内存容量可能撑不住了
    2. 跑完一次 epoch（全数据集）所需的迭代次数减少，要想达到相同的精度，其所花费的时间大大增加了，从而对参数的修正也就显得更加缓慢
    3. Batch_Size 增大到一定程度，其确定的下降方向已经基本不再变化

各种梯度下降法性能比较

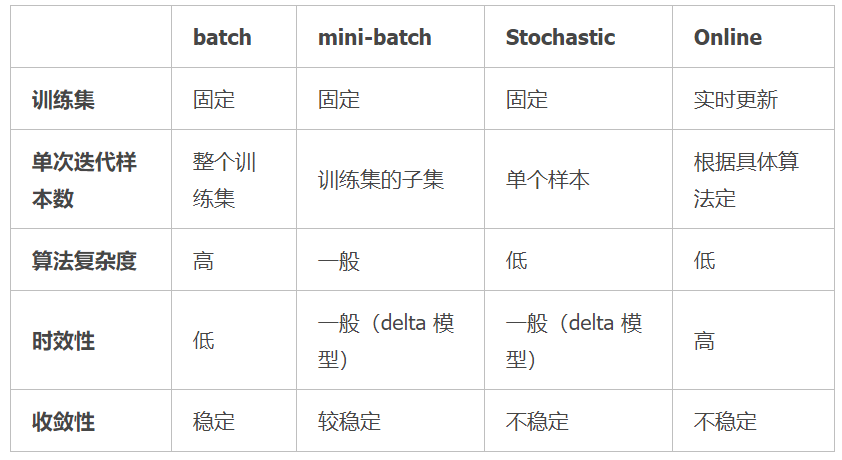
训 练 集 单 次 迭 代 样 本 数 算 法 复 杂 度 时 效 性 收 敛 性 batch 固 定 整 个 讠 川 练 集 稳 定 '-batch 固 定 训 练 集 的 子 集 一 般 (delta 模 较 稳 定 Stochastic 固 定 单 个 样 本 一 般 (delta 模 不 稳 定 Online 实 时 更 新 根 据 具 体 算 法 炬 不 稳 定

BGD、SGD、Mini-batchGD,前面均已讨论过，这里介绍一下 OnlineGD。

OnlineGD 于 mini-batchGD/SGD 的区别在于，所有训练数据只用一次，然后丢弃。这样做的优点在于可预测最终模型的变化趋势。

OnlineGD 在互联网领域用的较多，比如搜索广告的点击率(CTR)预估模型，网民的点击 行为会随着时间改变。用普通的 BGD 算法（每天更新一次）一方面耗时较长（需要对所有历 史数据重新训练）；另一方面，无法及时反馈用户的点击行为迁移。而 OnlineGD 算法可以实 时的依据网民的点击行为进行迁移。

模型评估

模型评估常用方法

一般情况来说，单一评分标准无法完全评估一个机器学习模型。只用 good 和 bad 偏离真 实场景去评估某个模型，都是一种欠妥的评估方式。下面介绍常用的分类模型和回归模型评估 方法。

分类模型常用评估方法

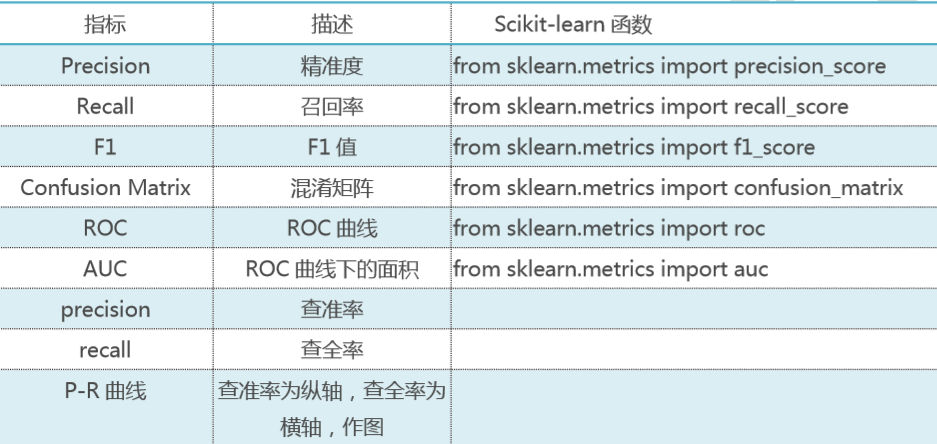
Precision Recall FI Confusion Matrix ROC AUC precision recall ROC ROC Scikit-learn from sklearn.metrics import precision_score from sklearn.metrics import recall_score from sklearn.metrics import fl_score from sklearn.metrics import confusion matrix from sklearn.metrics import roc from sklearn.metrics import auc

回归模型常用评估方法

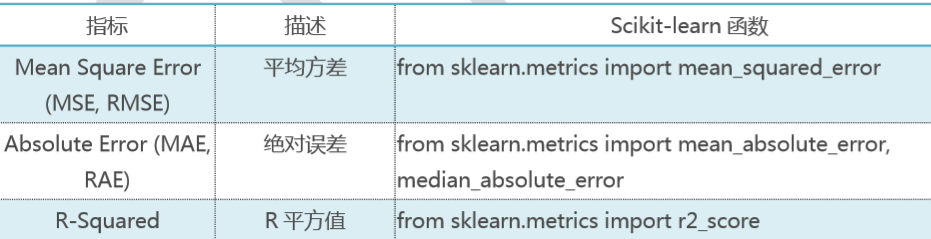
Mean Square Error (MSE, RMSE) Absolute Error (MAE, I RAE) R-Squared Scikit-learn from sklearn.metrics import mean_squared_error from sklearn.metrics import Imedian absolute error from sklearn.metrics import r2_score

经验误差与泛化误差

误差（error）：一般地，我们把学习器的实际预测输出与样本的真是输出之间的差异称为 “误差”

经验误差（empiricalerror）：也叫训练误差（trainingerror）。模型在训练集上的误差。

泛化误差（generalizationerror）：模型在新样本集（测试集）上的误差称为“泛化误差”。

偏差、方差、欠拟合、过拟合

偏差和方差

  • 偏差与方差分别是用于衡量一个模型泛化误差的两个方面；

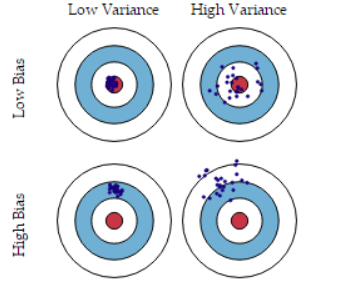
    • 模型的偏差，指的是模型预测的期望值与真实值之间的差；偏差越大，越偏离真实数据，如下图第二行所示。
    • 模型的方差，指的是模型预测的期望值与预测值之间的差平方和；描述的是预测值的变化范围，离散程度，也就是离其期望值的距离。方差越大，数据的分布越分散，模型的稳定程度越差。如果模型在训练集上拟合效果比较优秀， 但是在测试集上拟合效果比较差劣，则方差较大，说明模型的稳定程度较差，出现这种现象可 能是由于模型对训练集过拟合造成的。 如下图右列所示。

  • 在监督学习中，模型的泛化误差可分解为偏差、方差与噪声之和。

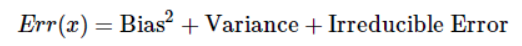
Err(x) Bias2 + Variance + Irreducible Error

  • 偏差用于描述模型的拟合能力；方差用于描述模型的稳定性。 简单的总结一下： 偏差大，会造成模型欠拟合； 方差大，会造成模型过拟合

АЭЭ

导致偏差和方差的原因

  1. 偏差通常是由于我们对学习算法做了错误的假设，或者模型的复杂度不够
    1. 比如真实模型是一个二次函数，而我们假设模型为一次函数，这就会导致偏差的增大（欠拟合）
    2. 由偏差引起的误差通常在训练误差上就能体现，或者说训练误差主要是由偏差造成的
  2. 方差通常是由于模型的复杂度相对于训练集过高导致的
    1. 比如真实模型是一个简单的二次函数，而我们假设模型是一个高次函数，这就会导致方差的增大（过拟合）
    2. 由方差引起的误差通常体现在测试误差相对训练误差的增量上

深度学习中的偏差与方差

  • 神经网络的拟合能力非常强，因此它的训练误差（偏差）通常较小；
  • 但是过强的拟合能力会导致较大的方差，使模型的测试误差（泛化误差）增大；
  • 因此深度学习的核心工作之一就是研究如何降低模型的泛化误差，这类方法统称为正则化方法。

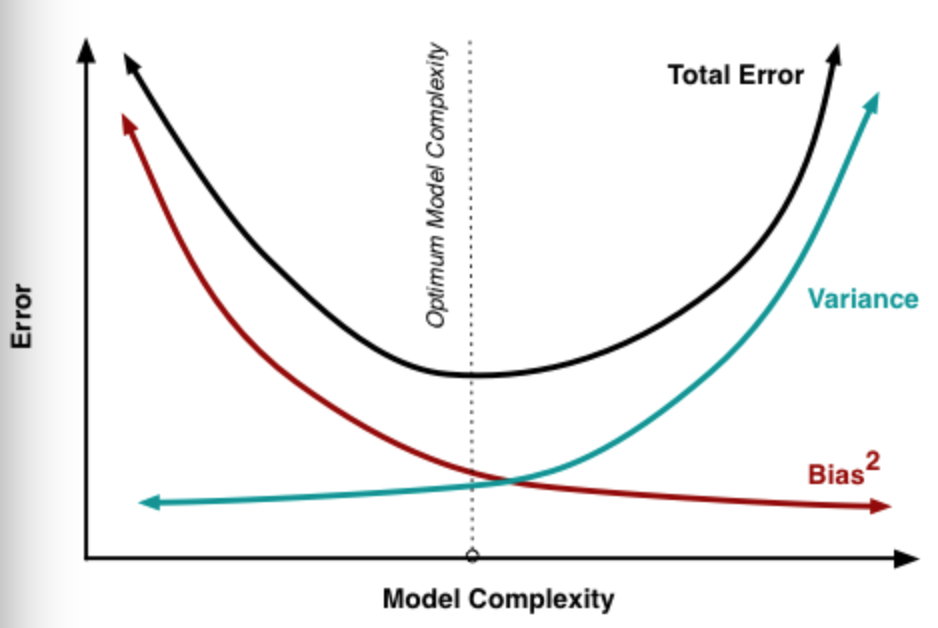
T0ta1 Error Variance 2 Bias Mode1 CompIexity

随着模型复杂度的增加，方差会逐渐增大，偏差会逐渐减小

欠拟合和过拟合定义

  • 模型欠拟合：在训练集以及测试集上同时具有较高的误差，此时模型的偏差较大；
  • 模型过拟合：在训练集上具有较低的误差，在测试集上具有较高的误差，此时模型的方差较大。
  • 模型正常：在训练集以及测试集上，同时具有相对较低的偏差以及方差。

图解

  • 横轴为模型复杂程度，纵轴为误差

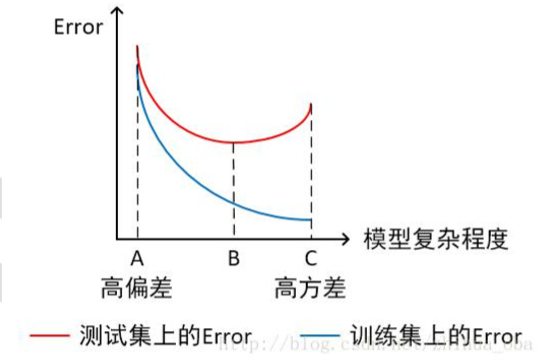
Error A 高 偏 差 B 测 试 集 上 的 Error 模 型 复 杂 程 度 C 高 方 差 训 练 集 上 的 Err 。 r

模型欠拟合：模型在点 A 处，在训练集以及测试集上同时具有较高的误差，此时模型的 偏差较大。

模型过拟合：模型在点 C 处，在训练集上具有较低的误差，在测试集上具有较高的误差， 此时模型的方差较大。 模型正常：模型复杂程度控制在点 B 处为最优。

  • 横轴为正则项系数，纵轴为误差

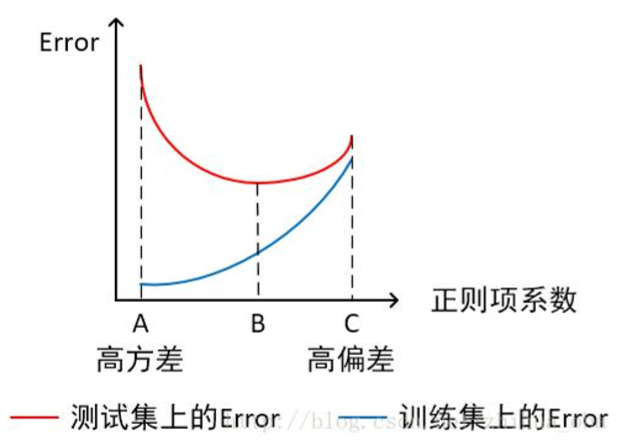
Error 正 则 项 系 数 A B 高 方 差 高 差 测 试 集 上 的 Error 训 练 集 上 的 Error

模型欠拟合：模型在点 C 处，在训练集以及测试集上同时具有较高的误差，此时模型的偏差较大。

模型过拟合：模型在点 A 处，在训练集上具有较低的误差，在测试集上具有较高的误差， 此时模型的方差较大。 模型正常：模型复杂程度控制在点 B 处为最优。

怎么判断是否过拟合，过拟合的曲线是什么样子的

  • train loss 不断下降，test loss不断下降，说明网络仍在学习;
  • train loss 不断下降，test loss趋于不变，说明网络过拟合;
  • train loss 趋于不变，test loss不断下降，说明数据集100%有问题;
  • train loss 趋于不变，test loss趋于不变，说明学习遇到瓶颈，需要减小学习率或批量数目;
  • train loss 不断上升，test loss不断上升，说明网络结构设计不当，训练超参数设置不当，数据集经过清洗等问题。

如何解决过拟合和欠拟合

如何解决欠拟合
  1. 添加其他特征项。组合、泛化、相关性、上下文特征、平台特征等特征是特征添加的重要手段，有时候特征项不够会导致模型欠拟合
  2. 添加多项式特征。例如将线性模型添加二次项或三次项使模型泛化能力更强。例如， FM 模型、FFM 模型，其实就是线性模型，增加了二阶多项式，保证了模型一定的拟合程度
  3. 可以增加模型的复杂程度
  4. 减小正则化系数。正则化的目的是用来防止过拟合的，但是现在模型出现了欠拟合， 则需要减少正则化参数
如何解决过拟合
  1. 重新清洗数据，数据不纯会导致过拟合，此类情况需要重新清洗数据
  2. 增加训练样本数量，数据增强
  3. 降低模型复杂程度
  4. 增大正则项系数
  5. 采用 dropout 方法，dropout 方法，通俗的讲就是在训练的时候让神经元以一定的概率不工作
  6. 提前终止（earlystoping）
  7. 减少迭代次数
  8. 增大学习率
  9. 添加噪声数据
  10. 树结构中，可以对树进行剪枝

欠拟合和过拟合这些方法，需要根据实际问题，实际模型，进行选择。

交叉验证

为了得到更为稳健可靠的模型，对模型的泛化误差进行评估，得到模型泛化误差的近似值。 当有多个模型可以选择时，我们通常选择“泛化误差”最小的模型。 交叉验证的方法有许多种，但是最常用的是：留一交叉验证、k 折交叉验证

k 折交叉验证

  1. 将含有 N 个样本的数据集，分成 K 份，每份含有 N/K 个样本。选择其中 1 份作为测试集，另外 K-1 份作为训练集，测试集就有 K 种情况
  2. 在每种情况中，用训练集训练模型，用测试集测试模型，计算模型的泛化误差
  3. 将 K 种情况下，模型的泛化误差取均值，得到模型最终的泛化误差

注：

  1. 一般 2<=K<=10。 k 折交叉验证的优势在于，同时重复运用随机产生的子样本进行训练和验证，每次的结果验证一次，10 折交叉验证是最常用的
  2. 训练集中样本数量要足够多，一般至少大于总样本数的 50%
  3. 训练集和测试集必须从完整的数据集中均匀取样。均匀取样的目的是希望减少训练集、 测试集与原数据集之间的偏差。当样本数量足够多时，通过随机取样，便可以实现均匀取样的效果

类别不平衡产生原因？

类别不平衡（class-imbalance）是指分类任务中不同类别的训练样例数目差别很大的情况。

产生原因： 通常分类学习算法都会假设不同类别的训练样例数目基本相同。如果不同类别的训练样例 数目差别很大，则会影响学习结果，测试结果变差。例如二分类问题中有 998 个反例，正例有 2 个，那学习方法只需返回一个永远将新样本预测为反例的分类器，就能达到 99.8%的精度； 然而这样的分类器没有价值。

常见的类别不平衡问题解决方法

防止类别不平衡对学习造成的影响，在构建分类模型之前，需要对分类不平衡性问题进行 处理。主要解决方法有：

扩大数据集

增加包含小类样本数据的数据，更多的数据能得到更多的分布信息。

对大类数据欠采样

减少大类数据样本个数，使与小样本个数接近。

缺点：欠采样操作时若随机丢弃大类样本，可能会丢失重要信息。

代表算法：EasyEnsemble。利用集成学习机制，将大类划分为若干个集合供不同的学习器 使用。相当于对每个学习器都进行了欠采样，但在全局来看却不会丢失重要信息。

对小类数据过采样

过采样：对小类的数据样本进行采样来增加小类的数据样本个数。

代表算法：SMOTE 和 ADASYN。

SMOTE：通过对训练集中的小类数据进行插值来产生额外的小类样本数据。 新的少数类样本产生的策略：对每个少数类样本 a，在 a 的最近邻中随机选一个样本 b， 然后在 a、b 之间的连线上随机选一点作为新合成的少数类样本。

ADASYN：根据学习难度的不同，对不同的少数类别的样本使用加权分布，对于难以学习的少数类的样本，产生更多的综合数据。 通过减少类不平衡引入的偏差和将分类决策边界 自适应地转移到困难的样本两种手段，改善了数据分布。

使用新评价指标

如果当前评价指标不适用，则应寻找其他具有说服力的评价指标。比如准确度这个评价指标在类别不均衡的分类任务中并不适用，甚至进行误导。因此在类别不均衡分类任务中，需要使用更有说服力的评价指标来对分类器进行评价。

选择新算法

不同的算法适用于不同的任务与数据，应该使用不同的算法进行比较。

数据代价加权

例如当分类任务是识别小类，那么可以对分类器的小类样本数据增加权值，降低大类样本的权值，从而使得分类器将重点集中在小类样本身上。

转化问题思考角度

例如在分类问题时，把小类的样本作为异常点，将问题转化为异常点检测或变化趋势检测问题。 异常点检测即是对那些罕见事件进行识别。变化趋势检测区别于异常点检测在于其通 过检测不寻常的变化趋势来识别。

将问题细化分析

对问题进行分析与挖掘，将问题划分成多个更小的问题，看这些小问题是否更容易解决。

归一化

为什么归一化能提高求解最优解速度

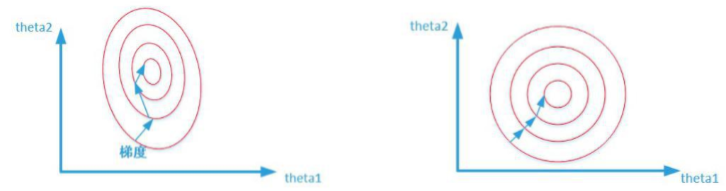
theta2

两张图代表数据是否均一化的最优解寻解过程（圆圈可以理解为等高线）。左图表示未经 归一化操作的寻解过程，右图表示经过归一化后的寻解过程。 当使用梯度下降法寻求最优解时，很有可能走“之字型”路线（垂直等高线走），从而导 致需要迭代很多次才能收敛；而右图对两个原始特征进行了归一化，其对应的等高线显得很圆， 在梯度下降进行求解时能较快的收敛。 因此如果机器学习模型使用梯度下降法求最优解时，归一化往往非常有必要，否则很难收 敛甚至不能收敛。

归一化类型

线性归一化

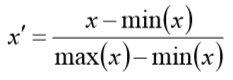
(х)шш хеш (х)шш — х

适用范围：比较适用在数值比较集中的情况。

缺点：如果 max 和 min 不稳定，很容易使得归一化结果不稳定，使得后续使用效果也不 稳定。

标准差归一化

img

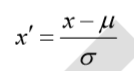
含义：经过处理的数据符合标准正态分布，即均值为 0，标准差为 1 其中μ为所有样本数 据的均值，σ为所有样本数据的标准差。

非线性归一化

适用范围：经常用在数据分化比较大的场景，有些数值很大，有些很小。通过一些数学函 数，将原始值进行映射。该方法包括 log、指数，正切等。

如何进行特征选择（feature selection）

如何考虑特征选择

当数据预处理完成后，我们需要选择有意义的特征输入机器学习的算法和模型进行训练。 通常来说，从两个方面考虑来选择特征：

  1. 特征是否发散：如果一个特征不发散，例如方差接近于 0，也就是说样本在这个特征上基本上没有差异，这个特征对于样本的区分并没有什么用。
  2. 特征与目标的相关性：这点比较显见，与目标相关性高的特征，应当优选选择。除 移除低方差法外，本文介绍的其他方法均从相关性考虑。

特征选择方法分类

根据特征选择的形式又可以将特征选择方法分为 3 种：

  1. Filter：过滤法，按照发散性或者相关性对各个特征进行评分，设定阈值或者待选择 阈值的个数，选择特征。
  2. Wrapper：包装法，根据目标函数（通常是预测效果评分），每次选择若干特征，或 者排除若干特征。
  3. Embedded：嵌入法，先使用某些机器学习的算法和模型进行训练，得到各个特征的 权值系数，根据系数从大到小选择特征。类似于 Filter 方法，但是是通过训练来确定特征的优劣。

特征选择目的

  1. 减少特征数量、降维，使模型泛化能力更强，减少过拟合；
  2. 增强对特征和特征值之间的理解。 拿到数据集，一个特征选择方法，往往很难同时完成这两个目的。通常情况下，选择一种 自己最熟悉或者最方便的特征选择方法（往往目的是降维，而忽略了对特征和数据理解的目的）。
FEATURED TAGS
机器学习 神经网络
FRIENDS