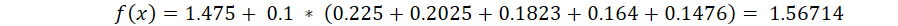GBDT
GBDT 的全称是 Gradient Boosting Decision Tree,梯度提升树,在传统机器学习算法中,GBDT算的上TOP3的算法。想要理解GBDT的真正意义,那就必须理解GBDT中的Gradient Boosting 和Decision Tree分别是什么?
Decision Tree:CART回归树
首先,GBDT使用的决策树是CART回归树,无论是处理回归问题还是二分类以及多分类,GBDT使用的决策树通通都是都是CART回归树。为什么不用CART分类树呢?因为GBDT每次迭代要拟合的是梯度值,是连续值所以要用回归树。
对于回归树算法来说最重要的是寻找最佳的划分点,那么回归树中的可划分点包含了所有特征的所有可取的值。在分类树中最佳划分点的判别标准是熵或者基尼系数,都是用纯度来衡量的,但是在回归树中的样本标签是连续数值,所以再使用熵之类的指标不再合适,取而代之的是平方误差,它能很好的评判拟合程度。
回归树生成算法:
输入:训练数据集D:
输出:回归树
在训练数据集所在的输入空间中,递归的将每个区域划分为两个子区域并决定每个子区域上的输出值,构建二叉决策树:
选择最优切分变量j与切分点s,求解
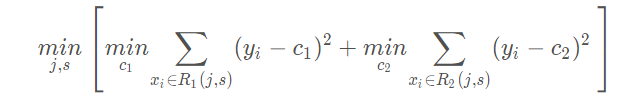
遍历变量j,对固定的切分变量j扫描切分点s,选择使得上式达到最小值的对。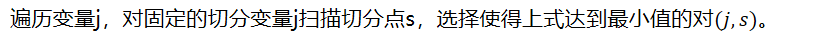
用选定的对划分区域并决定相应的输出值
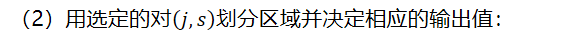
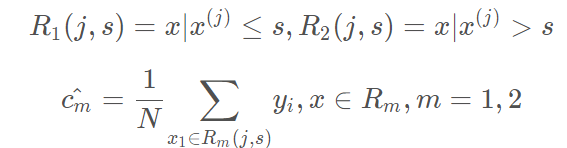
继续对两个子区域调用步骤(1)和(2),直至满足停止条件。
将输入空间划分为M 个区域 R1,R2,…RM,生成决策树:
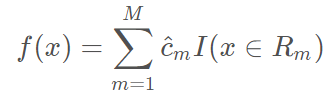
-————————————————————————————————————————————————————————————————————————————
Gradient Boosting
拟合负梯度
梯度提升树(Grandient Boosting)是提升树(Boosting Tree)的一种改进算法,所以在讲梯度提升树之前先来说一下提升树。
先来个通俗理解:假如有个人30岁,我们首先用20岁去拟合,发现损失有10岁,这时我们用6岁去拟合剩下的损失,发现差距还有4岁,第三轮我们用3岁拟合剩下的差距,差距就只有一岁了。如果我们的迭代轮数还没有完,可以继续迭代下面,每一轮迭代,拟合的岁数误差都会减小。最后将每次拟合的岁数加起来便是模型输出的结果
提升树算法
(1)初始化f0(x)=0
(2)对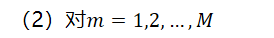
(a)计算残差
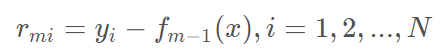
(b)拟合残差rmi 学习一个回归树,得到hm(x)
(c)更新 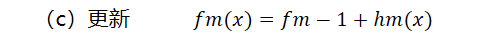
(3)得到回归问题提升树
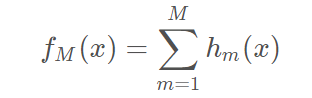
上面伪代码中的残差是什么?
在提升树算法中,假设我们前一轮迭代得到的强学习器是
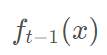
损失函数是
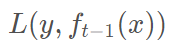
我们本轮迭代的目标是找到一个弱学习器
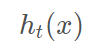
最小化本轮的损失
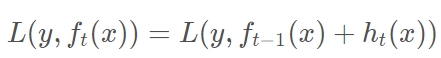
当采用平方损失函数时
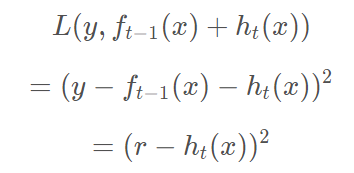
这里,
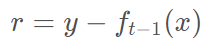
是当前模型拟合数据的残差(residual)所以,对于提升树来说只需要简单地拟合当前模型的残差。
回到我们上面讲的那个通俗易懂的例子中,第一次迭代的残差是10岁,第二 次残差4岁……
当损失函数是平方损失和指数损失函数时,梯度提升树每一步优化是很简单的,但是对于一般损失函数而言,往往每一步优化起来不那么容易,针对这一问题,Friedman提出了梯度提升树算法,这是利用最速下降的近似方法,其关键是利用损失函数的负梯度作为提升树算法中的残差的近似值。
那么负梯度长什么样呢?
第t轮的第i个样本的损失函数的负梯度为:
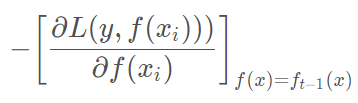
此时不同的损失函数将会得到不同的负梯度,如果选择平方损失
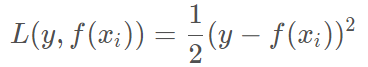
负梯度为
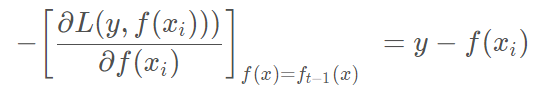
此时我们发现GBDT的负梯度就是残差,所以说对于回归问题,我们要拟合的就是残差。
那么对于分类问题呢?二分类和多分类的损失函数都是logloss,本文以回归问题为例进行讲解。
GBDT算法原理
上面两节分别将Decision Tree和Gradient Boosting介绍完了,下面将这两部分组合在一起就是我们的GBDT了。
GBDT算法:
(1)初始化弱学习器
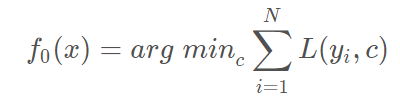
(2)对有: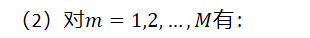
(a)对每个样本计算负梯度,即残差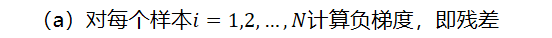
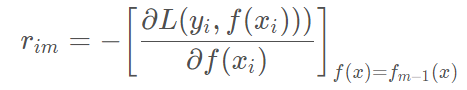
(b)将上步得到的残差作为样本新的真实值,并将数据(xi,rim),作为下棵树的训练数据,得到一颗新的回归树fm(x) ,其对应的叶子节点区域为Rjm,…,。其中J为回归树t的叶子节点的个数。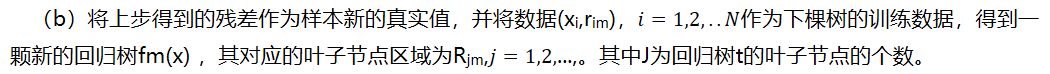
(c)对叶子区域计算最佳拟合值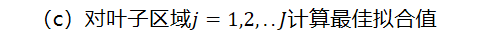
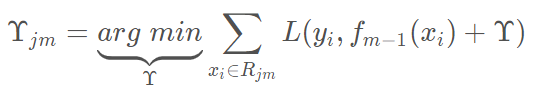
(d)更新强学习器
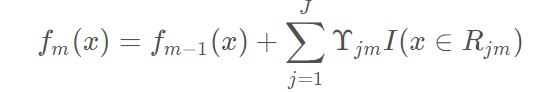
(3)得到最终学习器
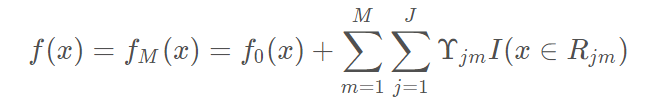
实例详解
数据介绍:
如下表所示:一组数据,特征为年龄、体重,身高为标签值。共有5条数据,前四条为训练样本,最后一条为要预测的样本。
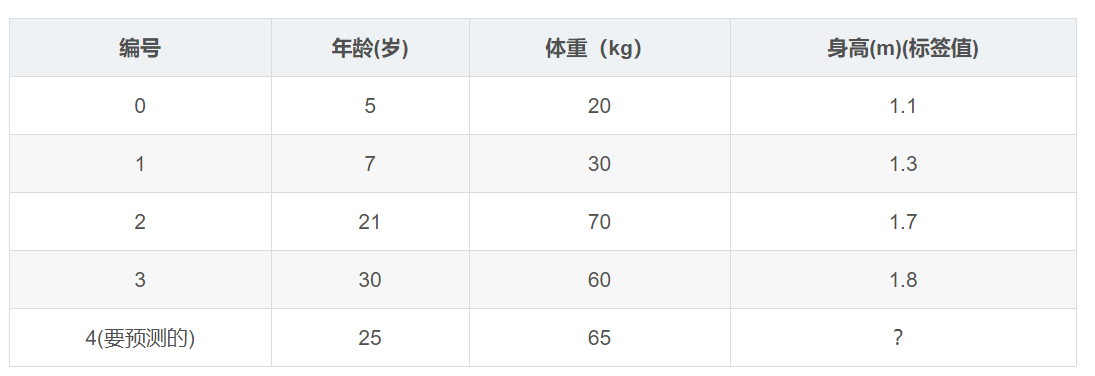
训练阶段:
参数设置:
- 学习率:learning_rate=0.1
- 迭代次数:n_trees=5
- 树的深度:max_depth=3
1.初始化弱学习器:
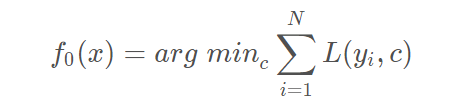
损失函数为平方损失,因为平方损失函数是一个凸函数,直接求导,倒数等于零,得到c。
令导数等于0
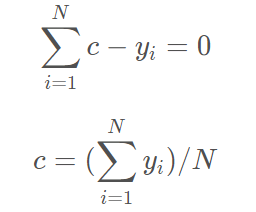
所以初始化时,c 取值为所有训练样本标签值的均值。,此时得到初始学习器f0(x)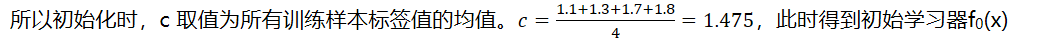
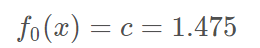
2.对迭代轮数m=1,2,…,M:
由于我们设置了迭代次数:n_trees=5,这里的M=5 。
计算负梯度,根据上文损失函数为平方损失时,负梯度就是残差残差,再直白一点就是 y 与上一轮得到的学习器fm−1的差值
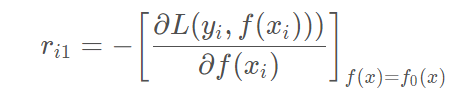
残差在下表列出:
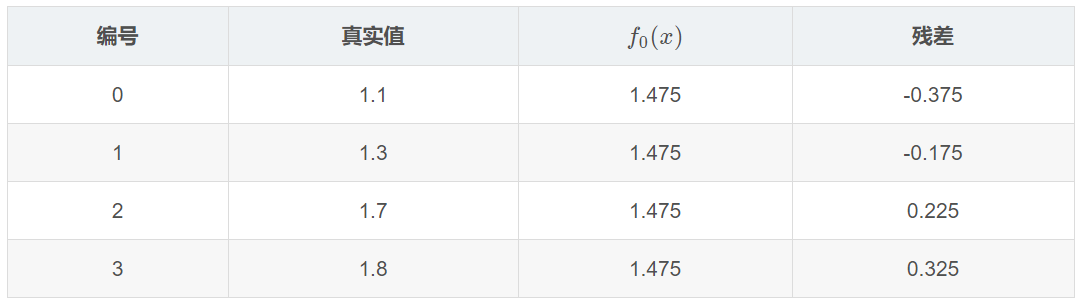
此时将残差作为样本的真实值来训练弱学习器f1(x) ,即下表数据
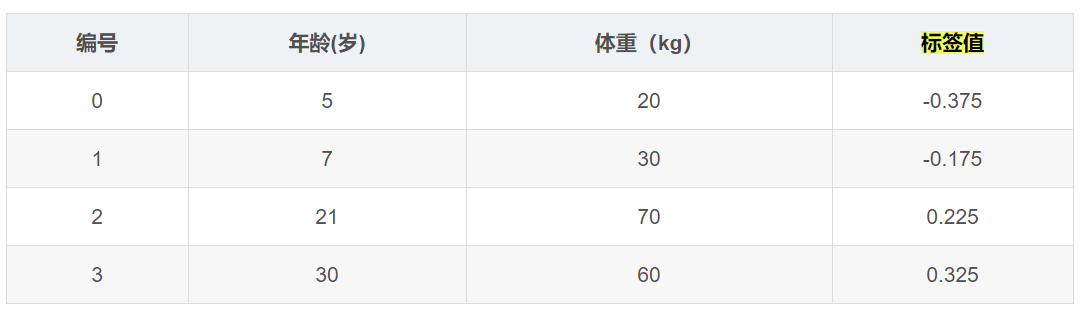
接着,寻找回归树的最佳划分节点,遍历每个特征的每个可能取值。从年龄特征的5开始,到体重特征的70结束,分别计算分裂后两组数据的平方损失(Square Error),SEl 左节点平方损失,SEr 右节点平方损失,找到使平方损失和SEsum=SEl+SEr最小的那个划分节点,即为最佳划分节点。
例如:以年龄7为划分节点,将小于7的样本划分为到左节点,大于等于7的样本划分为右节点。左节点包括x0,右节点包括样本x1,x2,x3 ,SEl=0, SEr=0.047, SEsum=0.047,所有可能划分情况如下表所示:
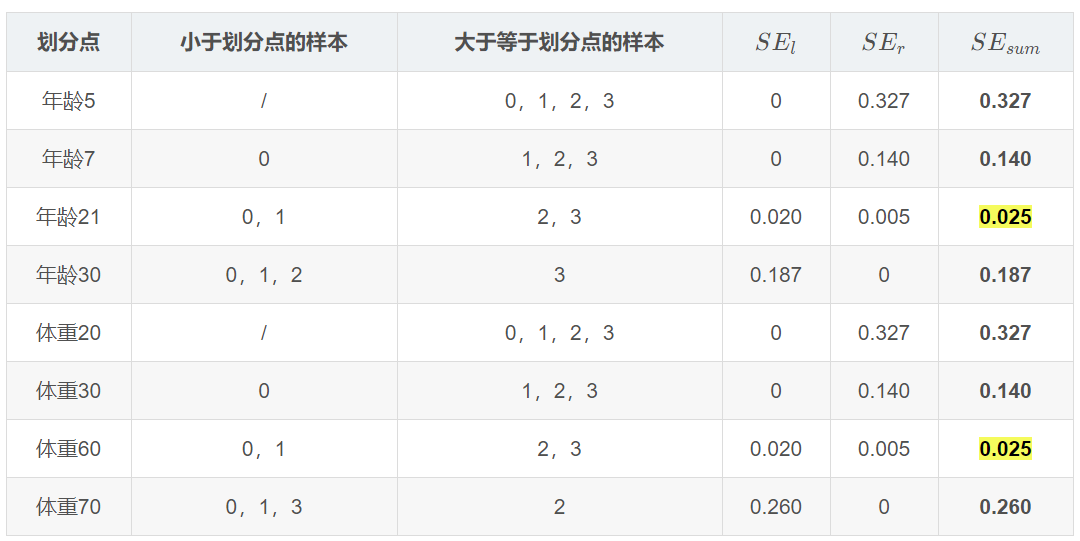
以上划分点是的总平方损失最小为0.025有两个划分点:年龄21和体重60,所以随机选一个作为划分点,这里我们选 年龄21, 现在我们的第一棵树长这个样子:
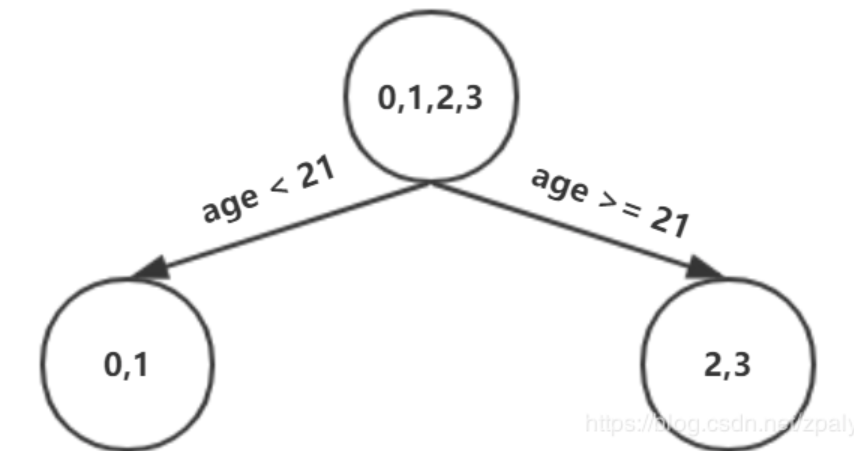
我们设置的参数中树的深度max_depth=3,现在树的深度只有2,需要再进行一次划分,这次划分要对左右两个节点分别进行划分:
对于左节点,只含有0,1两个样本,根据下表我们选择年龄7划分
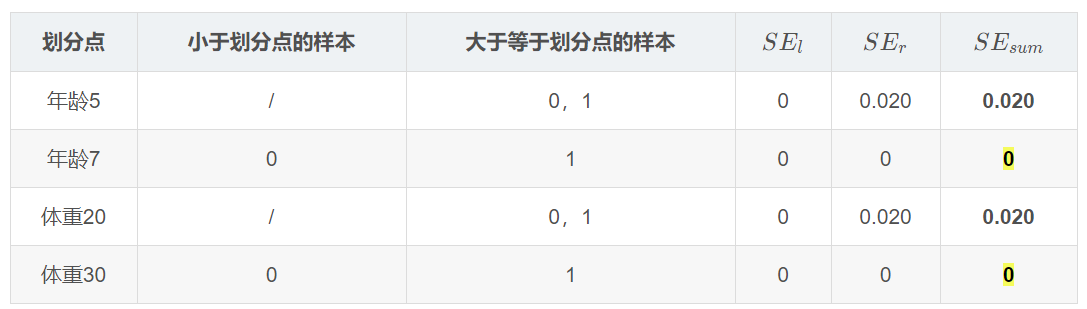
对于右节点,只含有2,3两个样本,根据下表我们选择年龄30划分(也可以选体重70)
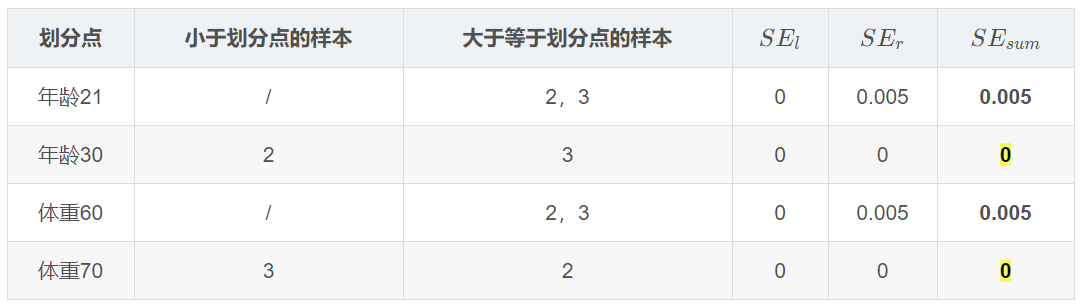
现在我们的第一棵树长这个样子:
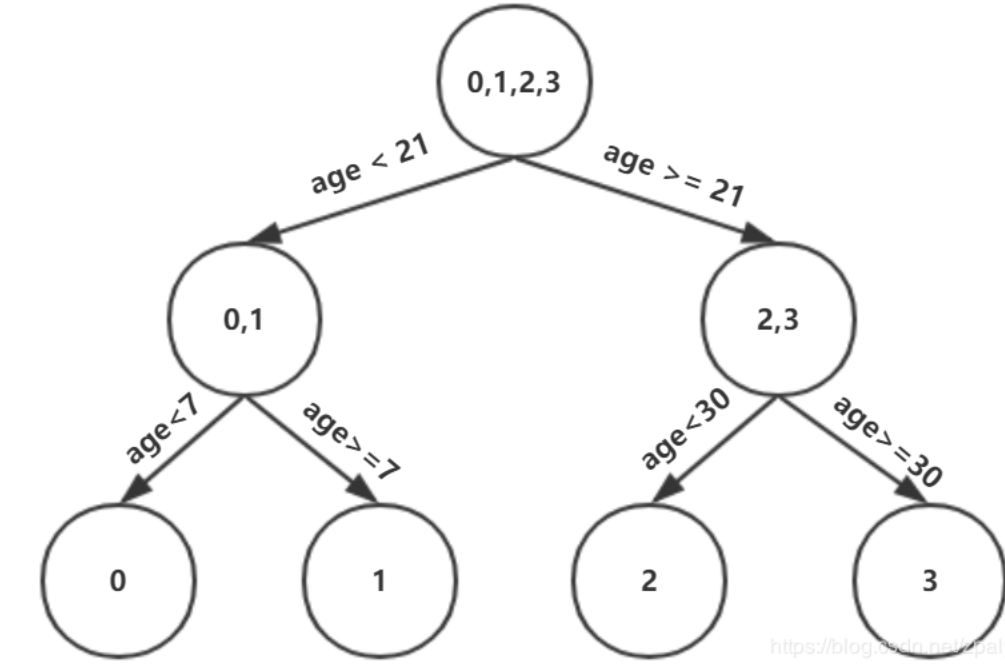
此时我们的树深度满足了设置,还需要做一件事情,给这每个叶子节点分别赋一个参数,来拟合残差。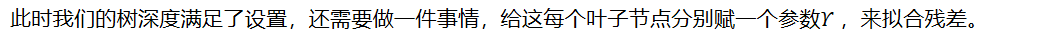
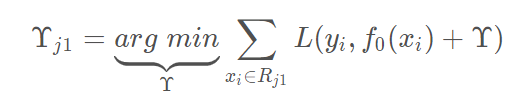
这里其实和上面初始化学习器是一个道理,平方损失,求导,令导数等于零,化简之后得到每个叶子节点的参数,其实就是标签值的均值。这个地方的标签值不是原始的 y,而是本轮要拟合的标残差
根据上述划分结果,为了方便表示,规定从左到右为第1,2,3,4个叶子结点
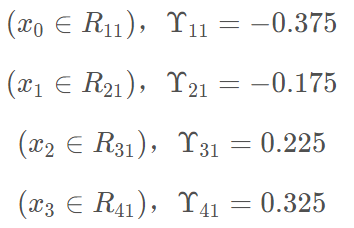
此时的树长这个样子:
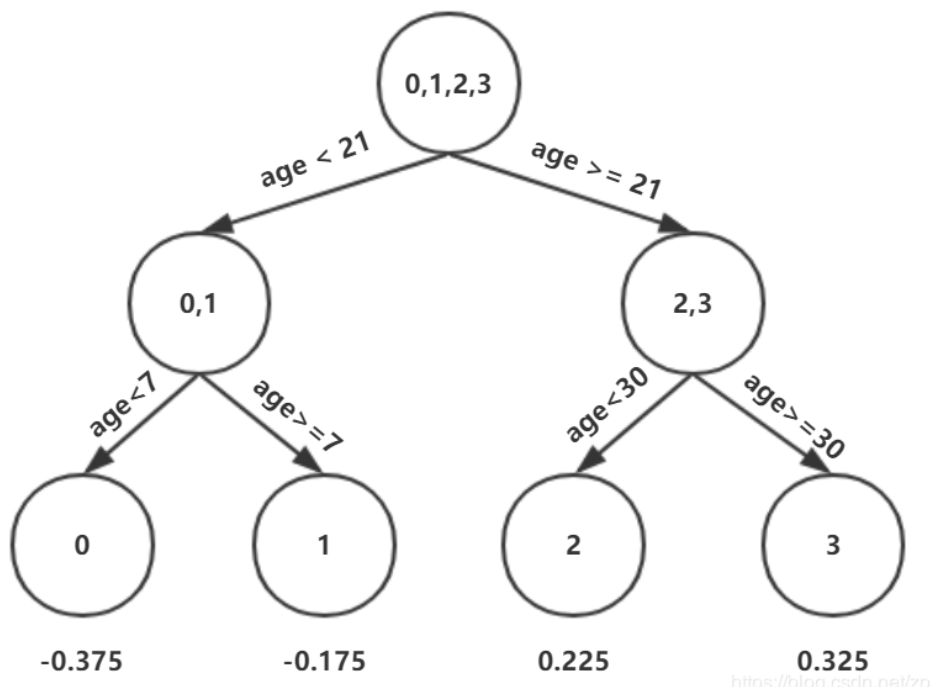
此时可更新强学习器,需要用到参数学习率:learning_rate=0.1,用lr表示
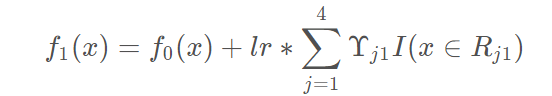
为什么要用学习率呢?这是Shrinkage的思想,如果每次都全部加上(学习率为1)很容易一步学到位导致过拟合。
重复此步骤,直到 m>5 结束,最后生成5棵树。
第一棵:
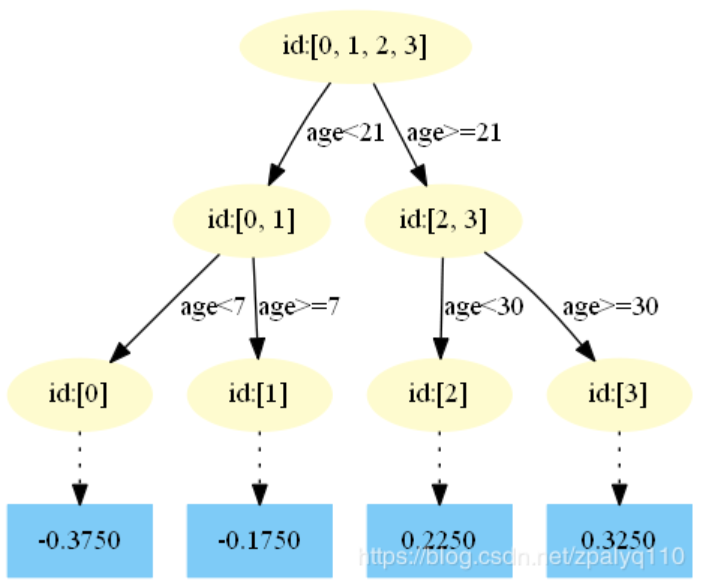
第二棵:
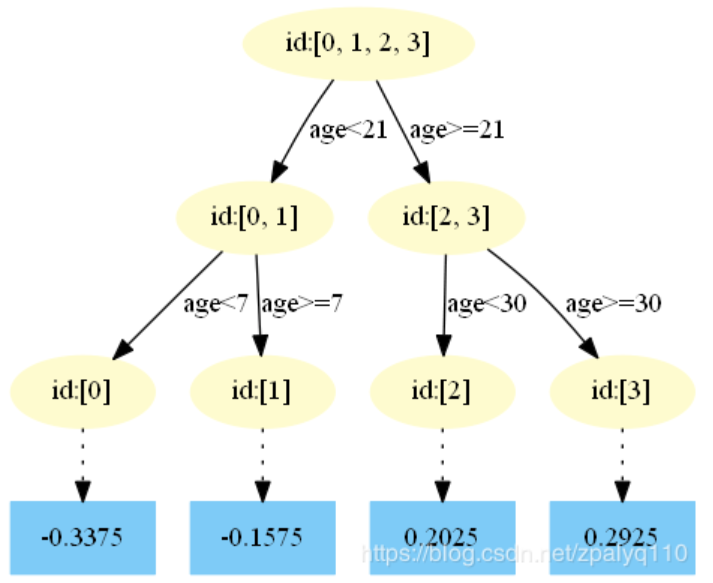
第三棵:
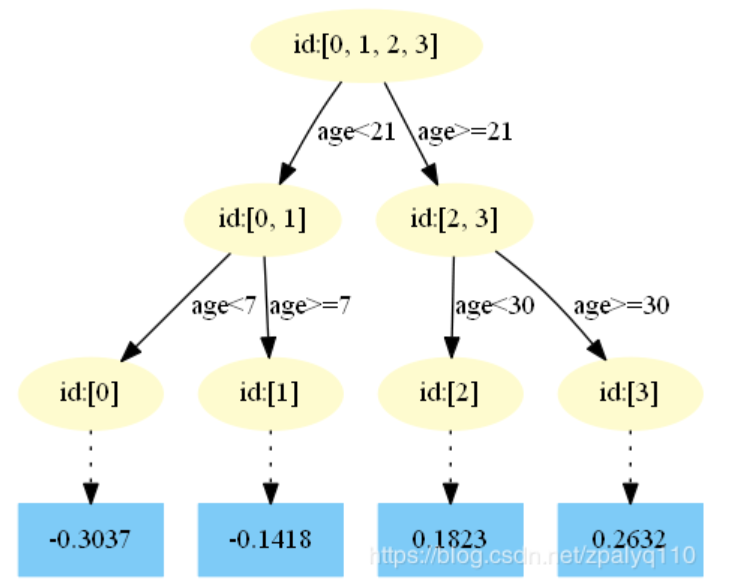
第四棵:
![id.[01 -0.2734 -0.1276 age<21 ages=21 id(2, 3] age<30 id(21 o. 1640 age>=30 0.2369](/2019/10/07/GBDT/clip_image051.png)
第五棵:
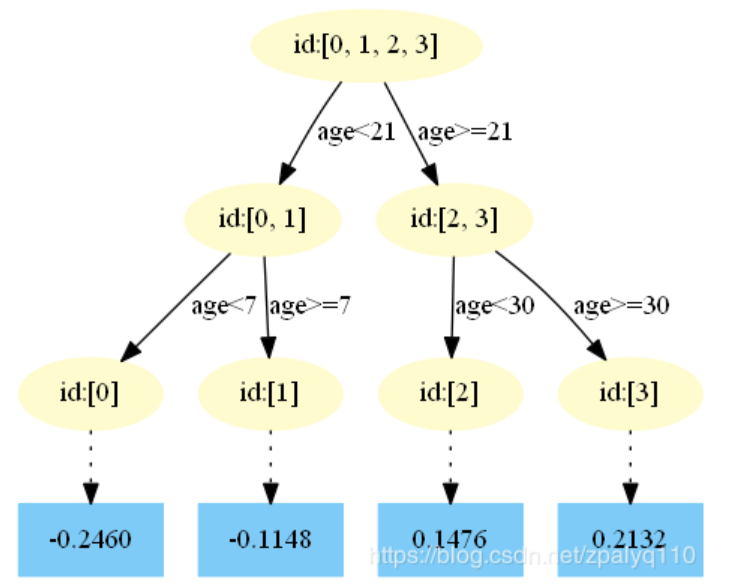
4.得到最后的强学习器:
![5 4 f (œ) f5(x) fo(‘œ) e R] m) m=l j=l ](file:///C:/Users/gaoming/AppData/Local/Temp/msohtmlclip1/01/clip_image053.png)
5.预测样本4:

在中,样本4的年龄为25,大于划分节点21岁,又小于30岁,所以被预测为0.2250。
在中,样本4的…此处省略…所以被预测为0.2025
为什么是0.2025?这是根据第二颗树得到的,可以GitHub简单运行一下代码
在中,样本4的…此处省略…所以被预测为0.1823
在中,样本4的…此处省略…所以被预测为0.1640
在中,样本4的…此处省略…所以被预测为0.1476
最终预测结果: