GBDT和XGBoost区别
牛顿法
GBDT 在函数空间中利用梯度下降法进行优化
XGBoost 在函数空间中用牛顿法进行优化
牛顿法看似比较陌生,在GBDT中梯度下降只是一阶泰勒公式展开,牛顿法就是二阶的泰勒公式展开,在参数空间中:

为了简化分析过程,假设参数是标量(即 只有一维),则可将一阶和二阶导数分别记为 g 和 h:
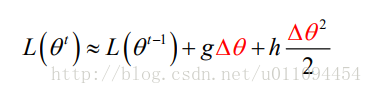

在函数空间中的牛顿法boosting与梯度boosting思想一样,只是f(x)函数变了:
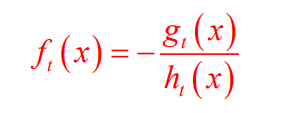
之后还是最终函数等于每次迭代的增量的累加和:
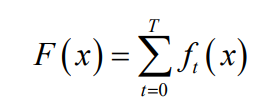
XGBOOST的目标函数
样本进行预测:
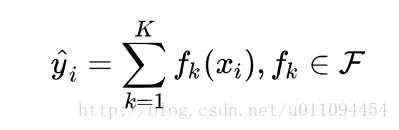
这里k是树的数量,是全部的回归树集合,而f就是其中一个回归树。

接下来看XGBOOST的目标函数,
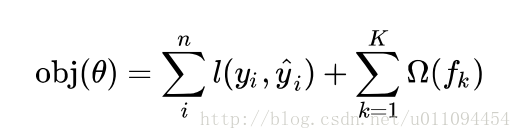

误差函数可以是square loss,logloss等,正则项可以是L1正则,L2正则等。
将y的预测值带入:
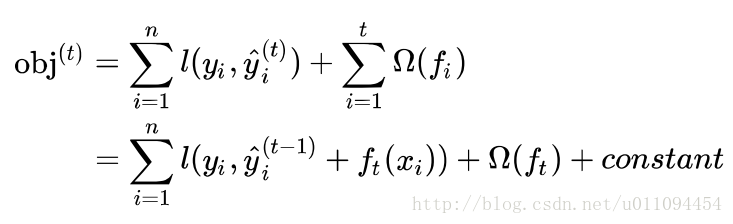
模型要学习的只有第t棵树 ,对进行二阶泰勒展开
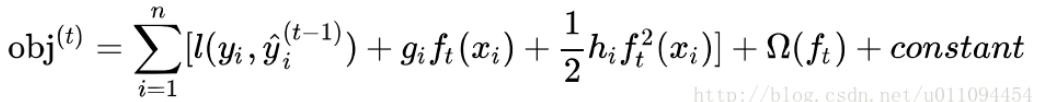
其中:
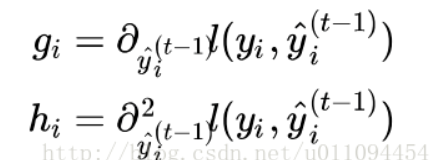
去掉其中的常数项:
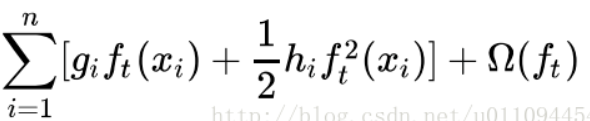
接下来讲公式的后面那个东西:正则项。
正则项
上面对GBDT中的分析可以知道它是没有正则项的,在XGBOOST中加入了正则项,但是正则项也不是XGBOOST首先加入的,并不是开创了先河。
正则项有什么作用呢?简单来说就是可以是的模型不容易过拟合。正则项对每棵回归树的复杂度进行了惩罚,而复杂度可以用树的深度,内部节点个数,叶子节点个数(T),叶节点分数(w)等来衡量。
首先对f(x)定义为:
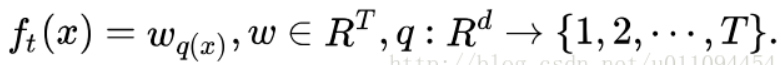
这个定义也要代入在整个目标函数中。在XGBOOST中,复杂度可以用:
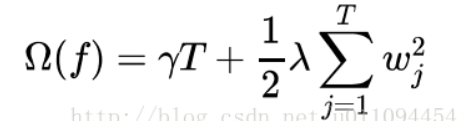
来表示,对叶子节点个数进行惩罚,相当于在训练过程中做了剪枝。
简化目标函数
带入正则项和f(x):
![obj gıWq@i) + îhiW2 ] + —A w2J .jzı ieıj ieıj ](file:///C:/Users/gaoming/AppData/Local/Temp/msohtmlclip1/01/clip_image018.png)
其中第一个约等于式子里:
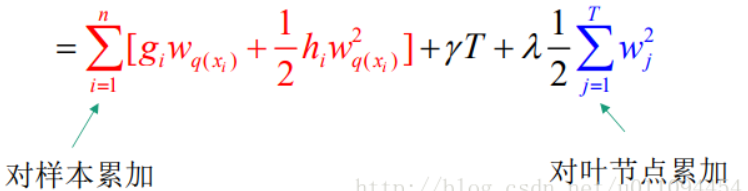
将它们统一起来,定义每个叶节点j上的样本集合:
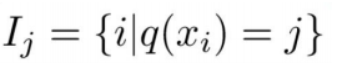
就成了后面的式子。定义:

可以得到:
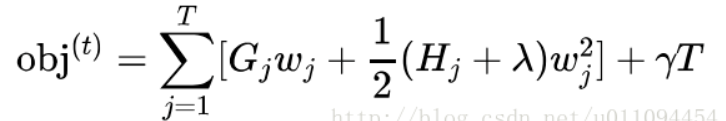
如果确定了树的结构(即q(x)确定),为了使目标函数最小,可以令其导数为0,解得每个叶节点的最优预测分数为:
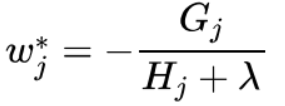
带入目标函数,得到最小损失函数,也就是我们的目标函数为:
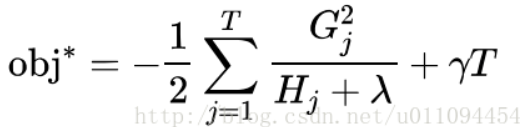
XGBOOST的打分函数
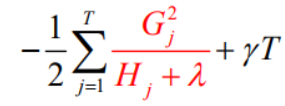
标红部分衡量了每个叶子节点对总体损失的的贡献,我们希望损失越小越好,则标红部分的值越大越好。
Gain函数:
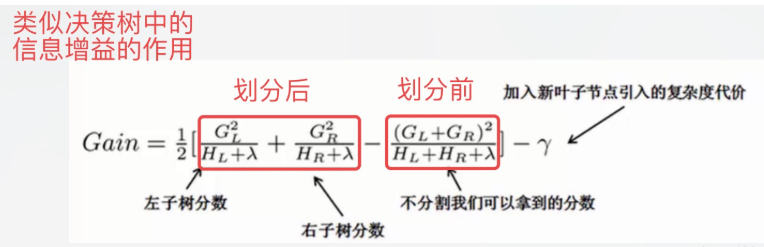
这个公式可以分解为:1)新左叶上的得分2)新右叶上的得分3)原叶上的得分4)附加叶上的正则化 ,所以当对一个叶节点分割时,计算所有候选(feature,value)对应的gain,选取gain最大的进行分割。
其他区别
Shrinkage(缩减):相当于学习速率(xgboost中的)。XGBoost在进行完一次迭代后,会将叶子节点的权重乘上该系数,主要是为了削弱每棵树的影响,让后面有更大的学习空间。实际应用中,一般把eta设置得小一点,然后迭代次数设置得大一点。(补充:传统GBDT的实现也有学习速率)
缺失值处理:XGBoost考虑了训练数据为稀疏值的情况,可以为缺失值或者指定的值指定分支的默认方向,这能大大提升算法的效率,paper提到50倍。即对于特征的值有缺失的样本,XGBoost可以自动学习出它的分裂方向。(通过枚举所有缺失值在当前节点是进入左子树,还是进入右子树更优来决定一个处理缺失值默认的方向)。
增益最大的那个特征去做分裂,那么各个特征的增益计算就可以开多线程进行。 XGBoost工具支持并行:Boosting不是一种串行的结构吗?怎么并行的?注意XGBoost的并行不是tree粒度的并行,XGBoost也是一次迭代完才能进行下一次迭代的(第次迭代的损失函数里包含了前面次迭代的预测值)。XGBoost的并行是在特征粒度上的。我们知道,决策树的学习最耗时的一个步骤就是对特征的值进行排序(因为要确定最佳分割点),XGBoost在训练之前,预先对数据进行了排序,然后保存为block(块)结构,后面的迭代中重复地使用这个结构,大大减小计算量。这个block结构也使得并行成为了可能,在进行节点的分裂时,需要计算每个特征的增益,最终选
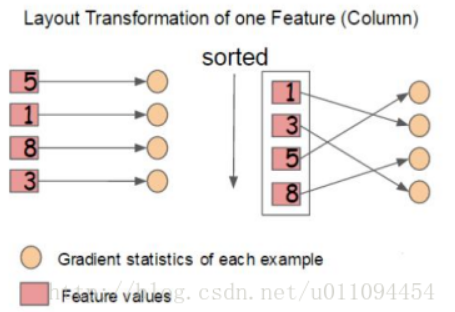
out-of-core 通过将block压缩(block compressoin)并存储到硬盘上,并且通过将block分区到多个硬盘上(block Sharding)实现了更大的IO 读写速度,因此,因为加入了硬盘存储block读写的部分不仅仅使得xgboost处理大数据量的能力有所提升,并且通过提高IO的吞吐量使得xgboost相比一般实利用这种技术实现大数据计算的框架更快。