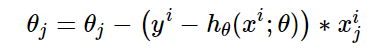线性回归和逻辑回归
线性回归
利用大量的样本
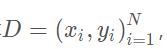
通过有监督的学习,学习到由x到y的映射f,利用该映射关系对未知的数据进行预估,因为y为连续值,所以是回归问题。
单变量情况
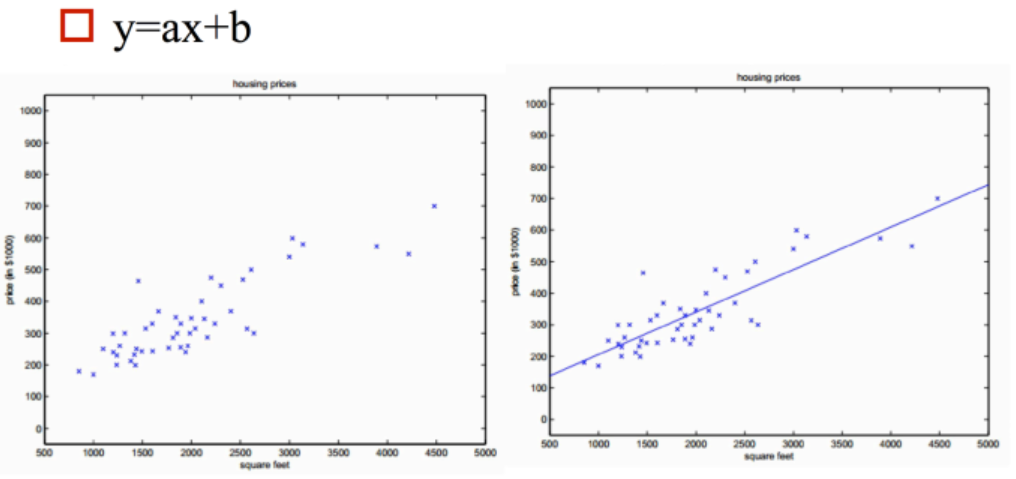
多变量情况
二维空间的直线,转化为高维空间的平面
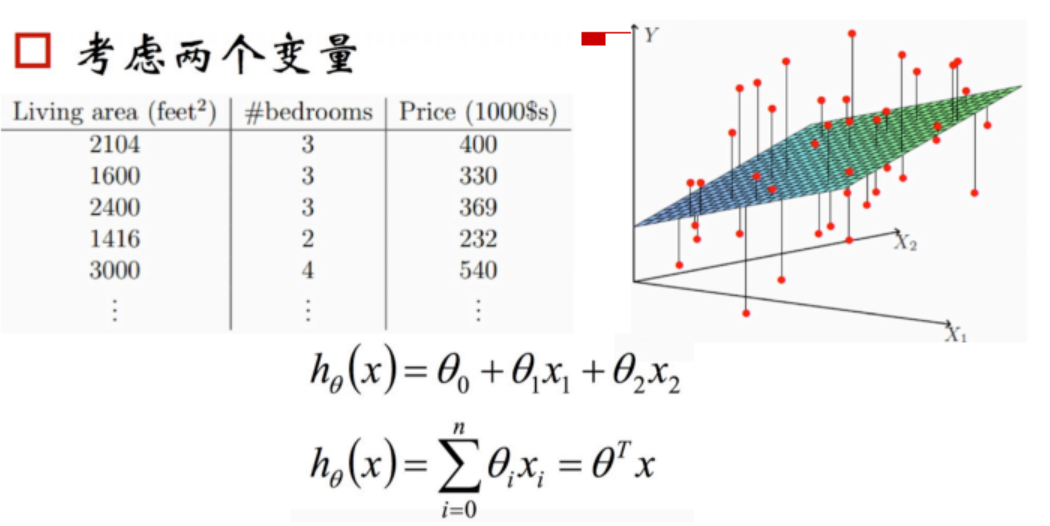
线性回归的表达式
机器学习是数据驱动的算法,数据驱动=数据+模型,模型就是输入到输出的映射关系。
模型=假设函数(不同的学习方式)+优化
假设函数
线性回归的假设函数(表示截距项,,方便矩阵表达):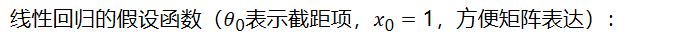
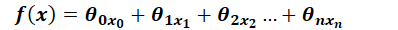
向量形式(都是列向量):
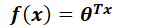
优化方法
监督学习的优化方法=损失函数+对损失函数的优化
损失函数
如何衡量已有的参数θ的好坏?
利用损失函数来衡量,损失函数度量预测值和标准答案的偏差,不同的参数有不同的偏差,所以要通过最小化损失函数,也就是最小化偏差来得到最好的参数。
映射函数: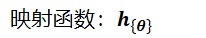
损失函数:
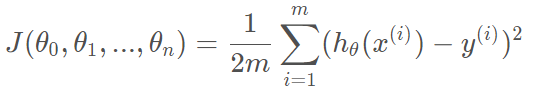
解释:因为有m个样本,所以要平均,分母的2是为了求导方便
损失函数:凸函数
解析式的求解过程
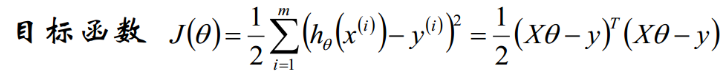
我们需要最小化目标函数,关心 取什么值的时候,目标函数取得最小值,而目标函数连续,那么 一定为 目标函数的驻点,所以我们求导寻找驻点。
求导可得:
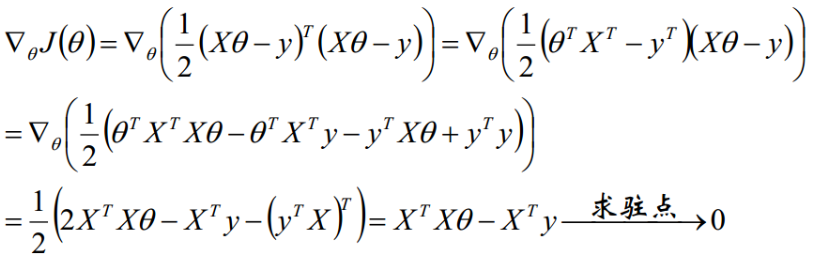
最终我们得到参数 的解析式:
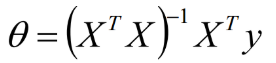
线性回归之梯度下降求解
求出代价函数关于的θ偏导(即梯度),最后按照梯度反方向来更新θ。公式推导如下:
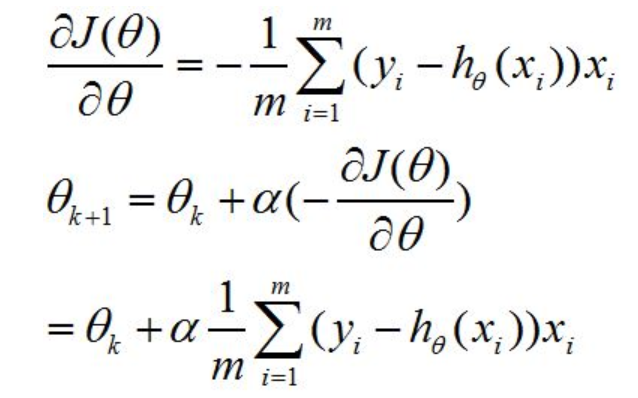
逻辑回归
Logistic回归的主要用途
- 寻找危险因素:寻找某一疾病的危险因素等
- 预测:根据模型,预测在不同的自变量情况下,发生某病或某种情况的概率有多大
- 判别:实际上跟预测有些类似,也是根据模型,判断某人属于某病或属于某种情况的概率有多大,也就是看一下这个人有多大的可能性是属于某病
常规步骤
Regression问题的常规步骤为:
- 寻找h函数(即hypothesis)
- 构造J函数(损失函数)
- 想办法使得J函数最小并求得回归参数(θ)
构造预测函数h
从名字来理解逻辑回归.在逻辑回归中,逻辑一词是logistics的音译字,并不是因为这个算法是突出逻辑的特性.
至于回归,我们前一段讲到回归任务是结果为连续型变量的任务,logistics regression是用来做分类任务的,为什么叫回归呢?那我们是不是可以假设,逻辑回归就是用回归的办法来做分类的呢.
假设刚刚的思路是正确的,逻辑回归就是在用回归的办法做分类任务,那有什么办法可以做到呢,此时我们就先考虑最简单的二分类,结果是正例或者负例的任务.
按照多元线性回归的思路,我们可以先对这个任务进行线性回归,学习出这个事情结果的规律,比如根据人的饮食,作息,工作和生存环境等条件预测一个人”有”或者”没有”得恶性肿瘤,可以先通过回归任务来预测人体内肿瘤的大小,取一个平均值作为阈值,假如平均值为y,肿瘤大小超过y为恶心肿瘤,无肿瘤或大小小于y的,为非恶性.这样通过线性回归加设定阈值的办法,就可以完成一个简单的二分类任务.如下图:
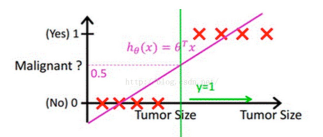
上图中,红色的x轴为肿瘤大小,粉色的线为回归出的函数的图像,绿色的线为阈值.
预测肿瘤大小还是一个回归问题,得到的结果(肿瘤的大小)也是一个连续型变量.通过设定阈值,就成功将回归问题转化为了分类问题.但是,这样做还存在一个问题.
我们上面的假设,依赖于所有的肿瘤大小都不会特别离谱,如果有一个超大的肿瘤在我们的例子中,阈值就很难设定.加入还是取平均大小为阈值,则会出现下图的情况:
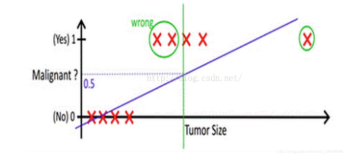
从上边的例子可以看出,使用线性的函数来拟合规律后取阈值的办法是行不通的,行不通的原因在于拟合的函数太直,离群值(也叫异常值)对结果的影响过大,但是我们的整体思路是没有错的,错的是用了太”直”的拟合函数,如果我们用来拟合的函数是非线性的,不这么直,是不是就好一些呢?
原来的判别函数我们用线性的y = wx, 逻辑回归的函数呢,我们目前就用sigmod函数,函数如下:
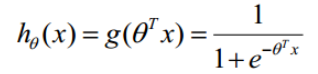
函数hθ(x) 的值有特殊的含义,它表示结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为:
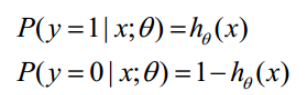
构造损失函数J
由上式可得似然函数:
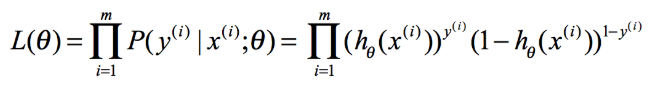
对数似然函数为:
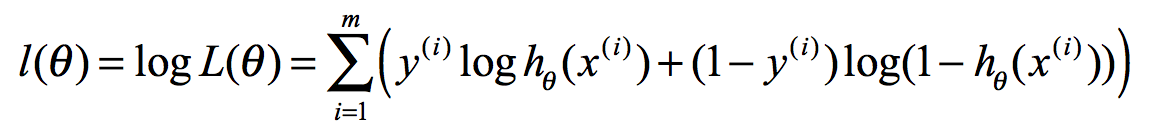
最大似然估计就是求使取最大值时的θ,将
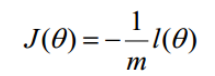
因为乘了一个负的系数-1/m,所以取最小值时的θ为要求的最佳参数。可用梯度下降求解。
梯度下降法求损失函数最小值
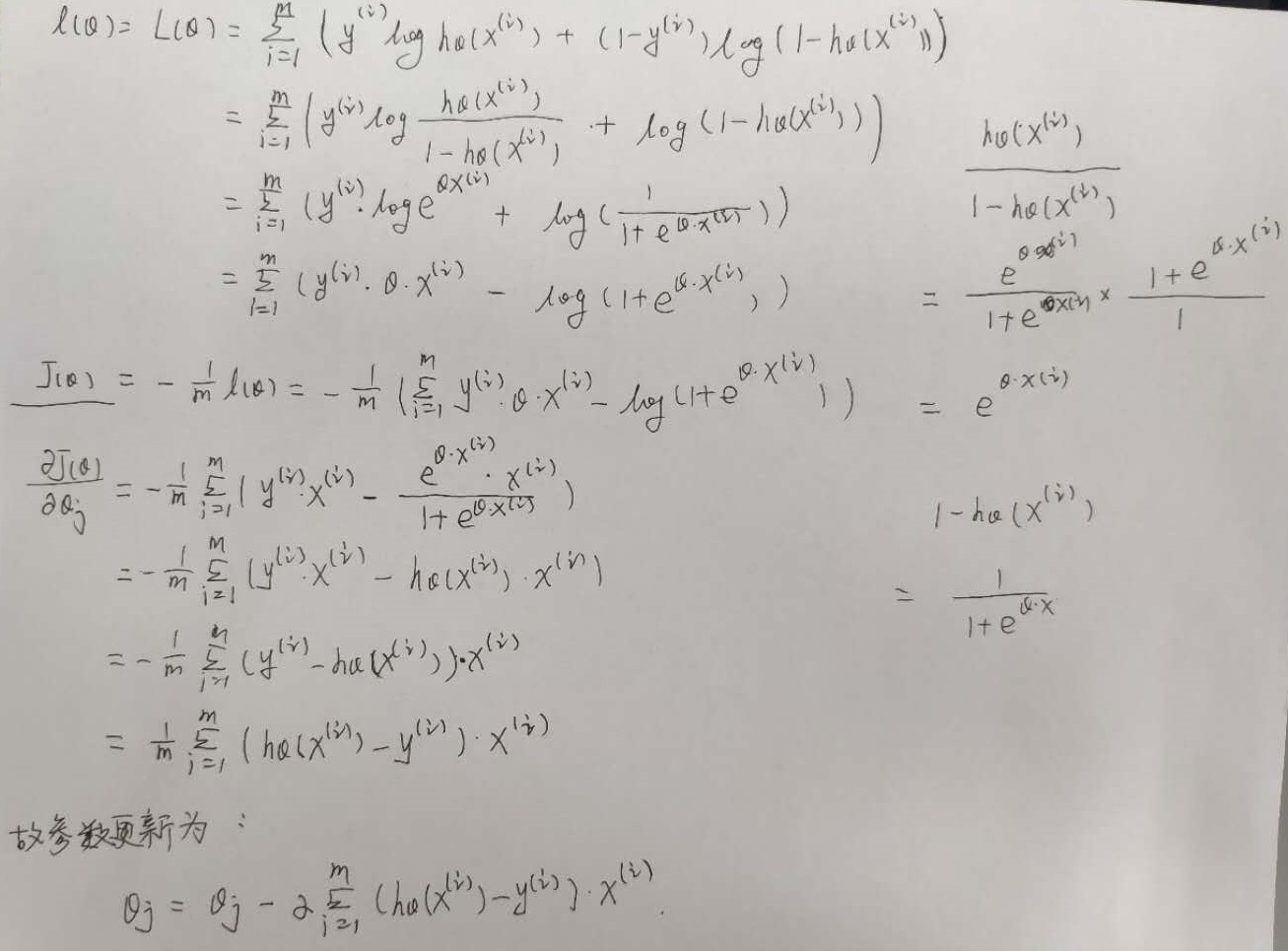
线性回归和逻辑回归的区别
- 线性回归要求变量服从正态分布,logistic回归对变量分布没有要求
- 线性回归要求自变量和因变量呈线性关系,而logistic回归不要求自变量和因变量呈线性关系
- 因变量不同:logistic回归是分析因变量取某个值的概率与自变量的关系,而线性回归是直接分析因变量与自变量的关系
Logistic Regression最大的特点就是将函数值收缩到[0,1]这个范围
面试问题
LR损失函数是什么,LR的梯度是如何表示的
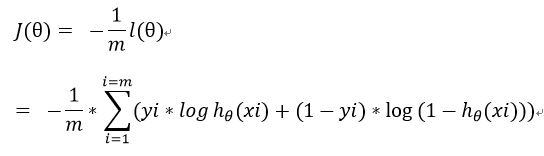
- 他为什么用log损失而不是均方误差损失(最小二乘**)** https://blog.csdn.net/zk_ken/article/details/82284723
在逻辑回归这个模型下,对数损失函数的训练求解参数的速度是比较快的。至于原因大家可以求出这个式子的梯度更新
这个式子的更新速度只和xij, y****i关。和sigmod函数本身的梯度是无关的。这样更新的速度是可以自始至终都比较的稳定。
为什么不选平方损失函数的呢?其一是因为如果你使用平方损失函数,你会发现梯度更新的速度和sigmod函数本身的梯度是很相关的。sigmod函数在它在定义域内的梯度都不大于0.25。这样训练会非常的慢。
如果根据似然函数,直接计算,有两点缺点:(1)不利于后续的求导,(2)似然函数的计算会导致下溢出。
逻辑回归不能解决什么问题
- 很难处理数据不平衡的问题。举个例子:如果我们对于一个正负样本非常不平衡的问题比如正负样本比 10000:1.我们把所有样本都预测为正也能使损失函数的值比较小。但是作为一个分类器,它对正负样本的区分能力不会很好。
逻辑回归在训练的过程当中,如果有很多的特征高度相关或者说有一个特征重复了100遍,会造成怎样的影响
- 先说结论,如果在损失函数最终收敛的情况下,其实就算有很多特征高度相关也不会影响分类器的效果。
- 但是对特征本身来说的话,假设只有一个特征,在不考虑采样的情况下,你现在将它重复100遍。训练以后完以后,数据还是这么多,但是这个特征本身重复了100遍,实质上将原来的特征分成了100份,每一个特征都是原来特征权重值的百分之一。
- 如果在随机采样的情况下,其实训练收敛完以后,还是可以认为这100个特征和原来那一个特征扮演的效果一样,只是可能中间很多特征的值正负相消了。
为什么我们还是会在训练的过程当中将高度相关的特征去掉
- 去掉高度相关的特征会让模型的可解释性更好
- 可以大大提高训练的速度。如果模型当中有很多特征高度相关的话,就算损失函数本身收敛了,但实际上参数是没有收敛的,这样会拉低训练的速度。其次是特征多了,本身就会增大训练的时间。
逻辑回归的优缺点总结
面试的时候,别人也经常会问到,你在使用逻辑回归的时候有哪些感受。觉得它有哪些优缺点。
在这里我们总结了逻辑回归应用到工业界当中一些优点:
形式简单,模型的可解释性非常好。从特征的权重可以看到不同的特征对最后结果的影响,某个特征的权重值比较高,那么这个特征最后对结果的影响会比较大。
模型效果不错。在工程上是可以接受的(作为baseline),如果特征工程做的好,效果不会太差,并且特征工程可以大家并行开发,大大加快开发的速度。
训练速度较快。分类的时候,计算量仅仅只和特征的数目相关。并且逻辑回归的分布式优化sgd发展比较成熟,训练的速度可以通过堆机器进一步提高,这样我们可以在短时间内迭代好几个版本的模型。
资源占用小,尤其是内存。因为只需要存储各个维度的特征值,。
方便输出结果调整。逻辑回归可以很方便的得到最后的分类结果,因为输出的是每个样本的概率分数,我们可以很容易的对这些概率分数进行cutoff,也就是划分阈值(大于某个阈值的是一类,小于某个阈值的是一类)。
但是逻辑回归本身也有许多的缺点:
准确率并不是很高。因为形式非常的简单(非常类似线性模型),很难去拟合数据的真实分布。
很难处理数据不平衡的问题。
处理非线性数据较麻烦。逻辑回归在不引入其他方法的情况下,只能处理线性可分的数据,或者进一步说,处理二分类的问题 。
逻辑回归本身无法筛选特征。有时候,我们会用gbdt来筛选特征,然后再上逻辑回归。
LR与SVM
https://blog.csdn.net/ccblogger/article/details/81711840
首先是两者的共同点:
- LR和SVM都是分类算法
- 如果不考虑核函数,LR和SVM都是线性分类算法,即分类决策面都是线性的
- LR和SVM都是有监督学习算法
- LR和SVM都是判别模型
两者的不同点:
- 损失函数的不同,逻辑回归采用的是log loss(对数损失函数),svm采用的是hinge loss(合页损失函数)
- 分类原理的不同,LR基于概率理论,通过极大似然估计的方法估计出参数的值,而SVM基于几何间隔最大化原理,认为存在最大几何间隔的分类面为最优分类面,从最大间隔出发,转化为求对变量w和b的凸二次规划问题
- 由于分类原理的不同,也导致了LR是所有样本都有影响,而SVM只是少量样本有影响的(支持向量),在支持向量外添加样本点是没有影响的
- 正因为LR受数据影响较大,所以在数据不同类别时,要先对数据做balancing
- 同样的,由于SVM依赖数据表达的距离测度,所以要先对数据做normalization标准化
- 对于线性不可分的情况,SVM的核函数可以帮助将低维不可分的数据转换到高维,变成线性可分的,而LR很少用到核函数(并不是没有。)假设我们在LR里也运用核函数的原理,那么每个样本点都必须参与核计算,这带来的计算复杂度是相当高的。所以,在具体应用时,LR很少运用核函数机制
- SVM的损失函数就自带正则(损失函数中的1/2||w||^2项),这就是为什么SVM是结构风险最小化算法的原因,而LR必须另外在损失函数上添加正则化
关于LR和SVM的选择:
- 如果Feature的数量很大,跟样本数量差不多,这时候选用LR或者是Linear Kernel的SVM
- 如果Feature的数量比较小,样本数量一般,不算大也不算小,选用SVM+Gaussian Kernel
- 如果Feature的数量比较小,而样本数量很多,需要手工添加一些feature变成第一种情况